Mathematics
A and B are points on a circle with center O. C is a point on the circle such that OC bisects ∠AOB, prove that OC bisects the arc AB.
Circles
46 Likes
Answer
The figure of the circle is shown below:

Given,
OC bisects ∠AOB.
∴ ∠AOC = ∠BOC
Since, equal arcs subtend equal angles at center.
∴ AC = BC
∴ C is mid-point of AB.
Hence, proved that OC bisects the arc AB.
Answered By
35 Likes
Related Questions
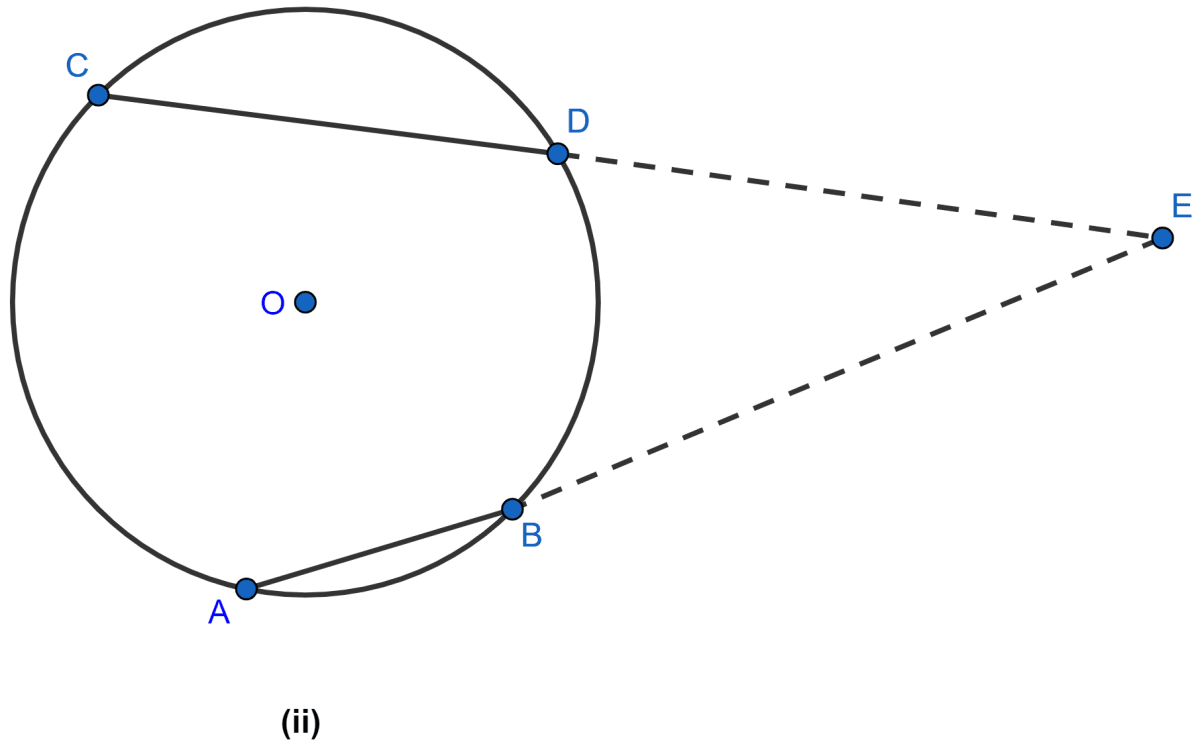
In the figure (ii) given below, AB and CD are equal chords of a circle with center O. If AB and CD meet at E (outside the circle) prove that
(i) AE = CE
(ii) BE = DE.
If arcs APB and CQD of a circle are congruent, then find the ratio of AB : CD.
Prove that the angle subtended at the center of a circle is bisected by the radius passing through the mid-point of arc.
In the adjoining figure, two chords AB and CD of a circle intersect at P. If AB = CD, prove that arc AD = arc CB.
