Mathematics
A closed box is a cuboid in shape with length = 40 cm, breadth = 30 cm and height = 50 cm. It is made of thin metal sheet. Find the cost of metal sheets required to make 20 such boxes, if 1 m2 of metal sheet costs ₹ 45.
Surface Area, Volume, Capacity
11 Likes
Answer
Given:
The length of the closed box = 40 cm = 0.4 m.
The breadth of the closed box = 30 cm = 0.3 m.
The height of the closed box = 50 cm = 0.5 m.
As we know, the total surface area of the cuboid = 2(l x b + b x h + h x l)
= 2(0.4 x 0.3 + 0.3 x 0.5 + 0.5 x 0.4) m2
= 2(0.12 + 0.15 + 0.2) m2
= 2 x 0.47 m2
= 0.94 m2
Total surface area of 20 boxes = Surface area of 1 box 20
= 0.94 x 20 m2
= 18.8 m2
Cost of 1 m2 sheet = ₹ 45
Total cost = Total surface area x Cost of 1 m2 sheet
= ₹ 18.8 x 45
= ₹ 846
Hence, the total cost of the sheet is ₹ 846.
Answered By
6 Likes
Related Questions
A wall 9 m long, 6 m high and 20 cm thick, is to be constructed using bricks of dimensions 30 cm, 15 cm and 10 cm. How many bricks will be required ?
A solid cube of edge 14 cm is melted down and recast into smaller and equal cubes each of edge 2 cm. Find the number of smaller cubes obtained.
Four cubes, each of edge 9 cm, are joined as shown below :
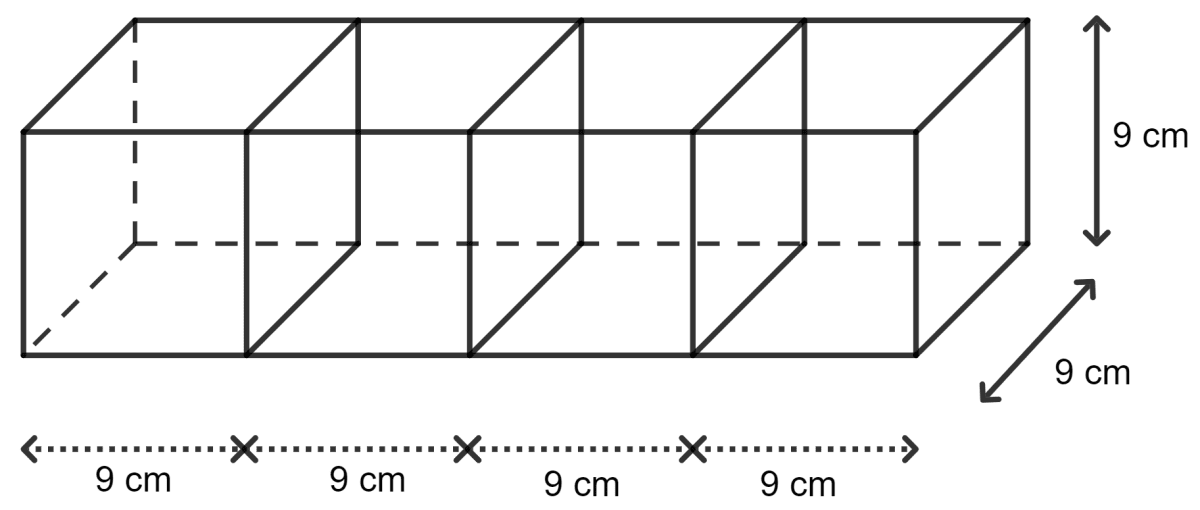
Write the dimensions of the cuboid obtained. Also, find total surface area and volume.
What is the maximum length of a rod which can be kept in a rectangular box with internal dimensions 32 cm x 24 cm x 8 cm.