A line parallel to side BC of a triangle ABC, intersects AB and AC at D and E respectively. Prove that $\dfrac{AD}{DB} = \dfrac{AE}{EC}$.

ΔABC with DE parallel to BC and intersecting AB and AC at D and E respectively is shown in the figure below:

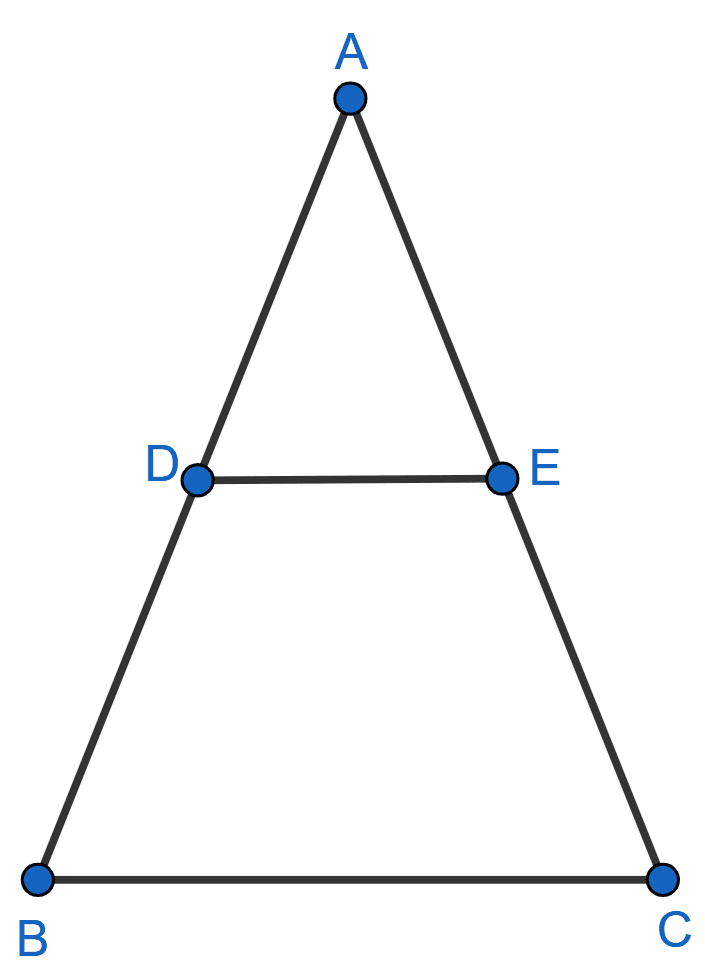
Join the vertex B of Δ ABC to E and the vertex C to D to form the lines BE and CD and then drop a perpendicular EN to the side AB and also draw DM ⊥ AC.

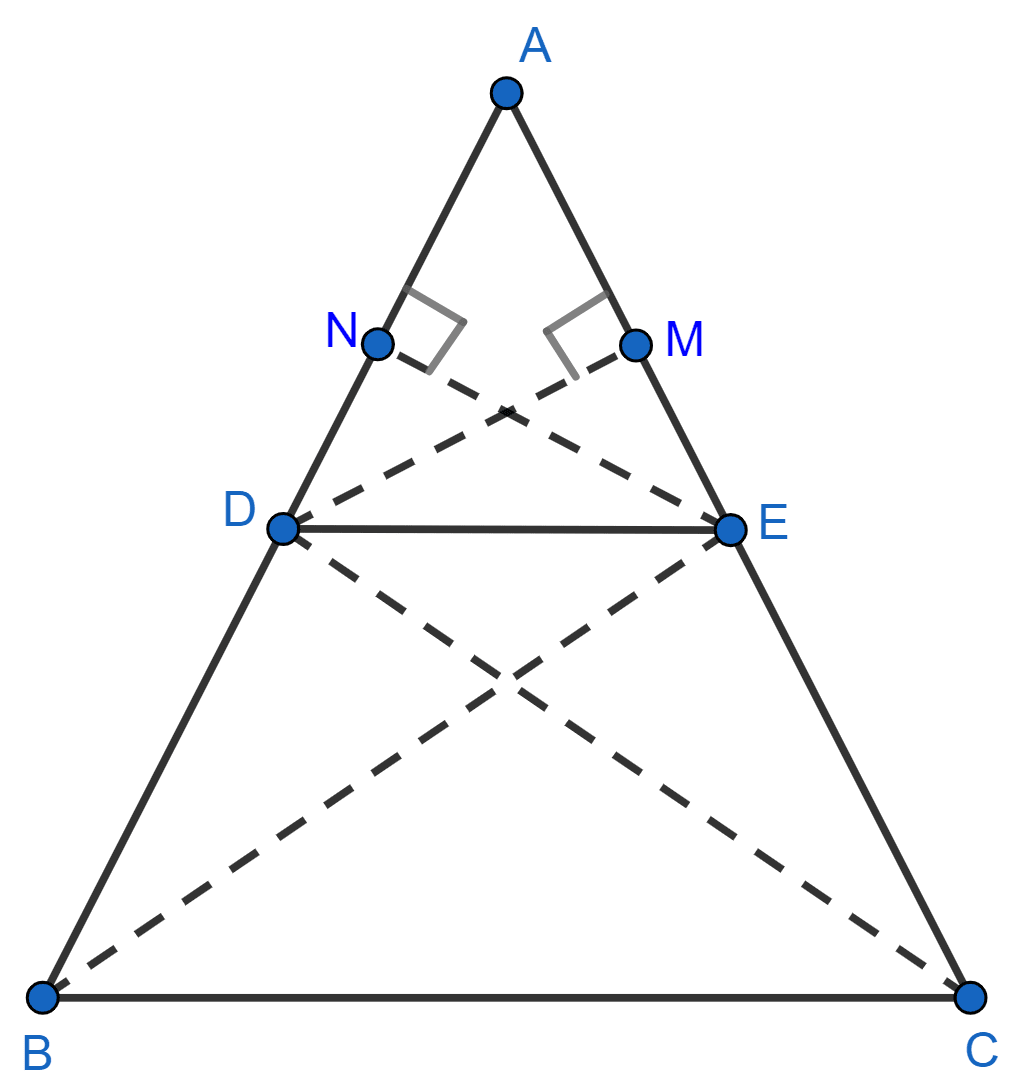
Area of Δ = $\dfrac{1}{2} \times$ Base × Height

Area of Δ ADE = $\dfrac{1}{2} \times AD \times EN$ ……….(1)

Area of Δ BDE = $\dfrac{1}{2} \times DB \times EN$ ……….(2)

Area of Δ ADE = $\dfrac{1}{2} \times AE \times DM$ ……….(3)

Area of Δ DEC = $\dfrac{1}{2} \times EC \times DM$ ………..(4)

Dividing equations (1) and (2), we get :

$\Rightarrow \dfrac{\text{Area of Δ ADE}}{\text{Area of Δ BDE}} = \dfrac{\dfrac{1}{2} \times AD \times EN}{\dfrac{1}{2} \times DB \times EN} \\[1em] = \dfrac{AD}{DB} ………..(5)$

Dividing equations (3) and (4), we get :

$\Rightarrow \dfrac{\text{Area of Δ ADE}}{\text{Area of Δ DEC}} = \dfrac{\dfrac{1}{2} \times AE \times DM}{\dfrac{1}{2} \times EC \times DM} \\[1em] = \dfrac{AE}{EC} ………..(6)$

From figure,

Δ BDE and Δ DEC are on the same base DE and between the same parallel lines BC and DE.

∴ Area of △ BDE = Area of △ DEC

$\therefore \dfrac{AD}{DB} = \dfrac{AE}{EC}$ ……….[From (5) and (6)]

Hence, proved that $\dfrac{AD}{DB} = \dfrac{AE}{EC}$.