Physics
A ray of light of wavelength 5400 Å suffers refraction from air to glass. Taking aμg = 3/2, find the wavelength of light in glass.
Refraction Plane Surfaces
52 Likes
Answer
As we know that,
Given,
Refractive index of glass with respect to air is given by aμg =
Wavelength of light in air = 5400 Å
Substituting the values in the formula above we get,
Hence, wavelength of light in glass = 3600 Å
Answered By
31 Likes
Related Questions
What device other than a plane mirror, can be used to turn a ray of light through 180°? Draw a diagram in support of your answer. Name an instrument in which this device is used.
Two isosceles right-angled glass prisms P and Q are placed near each other as shown in figure. Complete the path of the light ray entering the prism P till it emerges out of the prism Q.
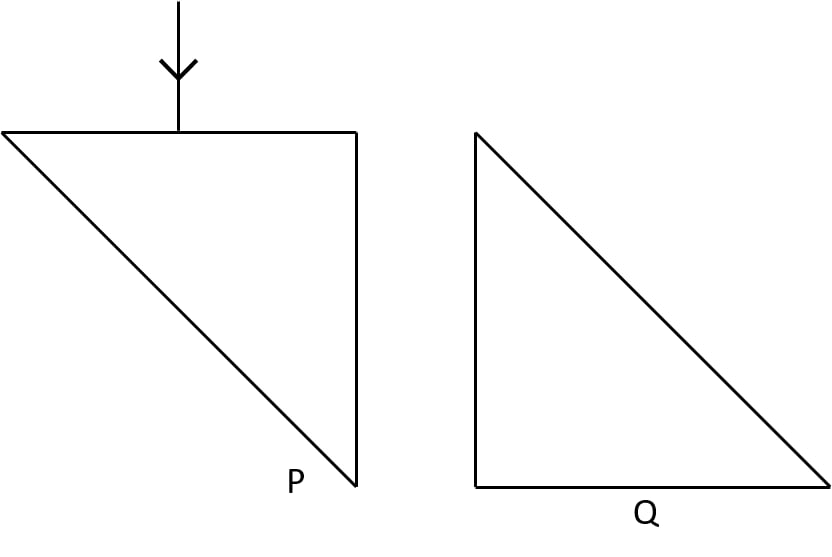
Complete the path of ray PQ through the glass prism ABC as shown in figure till it emerges out of the prism. Given the critical angle of glass is 42°.
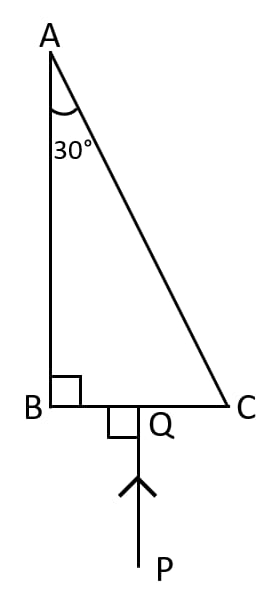
The diagram below shows a light source P embedded in a rectangular glass block ABCD of critical angle 42°. Complete the path of the ray PQ till it emerges out of the block. [Write necessary angles.]
![The diagram below shows a light source P embedded in a rectangular glass block ABCD of critical angle 42°. Complete the path of the ray PQ till it emerges out of the block. [Write necessary angles.] ICSE 2019 Physics Solved Question Paper.](https://cdn1.knowledgeboat.com/img/abp10/5/icse-2019-physics-question-paper-solved-2e-1200x730.png)