Mathematics
A straight line passes through P(2, 1) and cuts the axes in points A, B. If BP : PA = 3 : 1.

Find :
(i) the coordinates of A and B.
(ii) the equation of the line AB.
Straight Line Eq
44 Likes
Answer
A lies on x-axis and B lies on y-axis. Let coordinates of A be (x, 0) and B be (0, y) and P(2, 1) divides BA in the ratio 3 : 1.
By section formula,
Similarly,
Hence, coordinates of A are and of B are (0, 4).
(ii) By two point formula equation of AB will be,
Hence, the equation of the required line is 3x + 2y = 8.
Answered By
27 Likes
Related Questions
The points A(7, 3) and C(0, -4) are two opposite vertices of a rhombus ABCD. Find the equation of the diagonal BD.
A and B are two points on the x-axis and y-axis respectively.
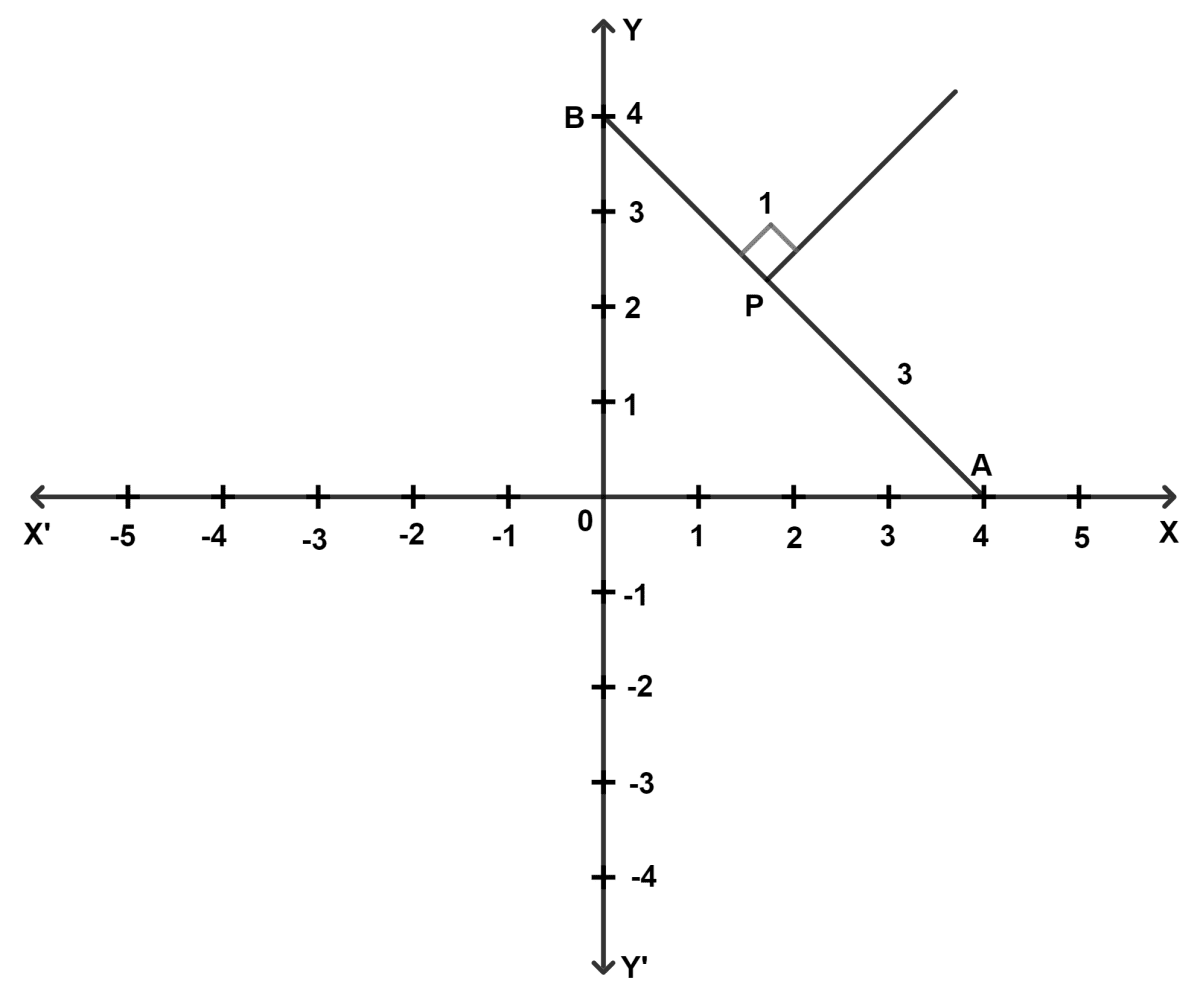
(a) Write down the co-ordinates of A and B.
(b) P is a point on AB such that AP : PB = 3 : 1. Using section formula find the coordinates of point P.
(c) Find the equation of a line passing through P and perpendicular to AB.
A straight line makes on the coordinate axes positive intercepts whose sum is 7. If the line passes through the point (-3, 8), find its equation.
If the coordinates of the vertex A of a square ABCD are (3, -2) and the equation of diagonal BD is 3x - 7y + 6 = 0, find the equation of the diagonal AC. Also find the coordinates of the centre of the square.