A thin rectangular card board has dimensions 44 cm x 22 cm. It is rolled along its length to get a hollow cylinder of largest size. Find the volume of the cylinder formed.

Clearly, length of the rectangular sheet = Circumference of the base of the cylinder formed

$⇒ 2πr = 44\\[1em] ⇒ 2 \times \dfrac{22}{7} \times r = 44\\[1em] ⇒ \dfrac{44}{7} \times r = 44\\[1em] ⇒ r = \dfrac{7 \times 44}{44}\\[1em] ⇒ r = \dfrac{7 \times \cancel{44}}{\cancel{44}}\\[1em] ⇒ r = 7 cm$

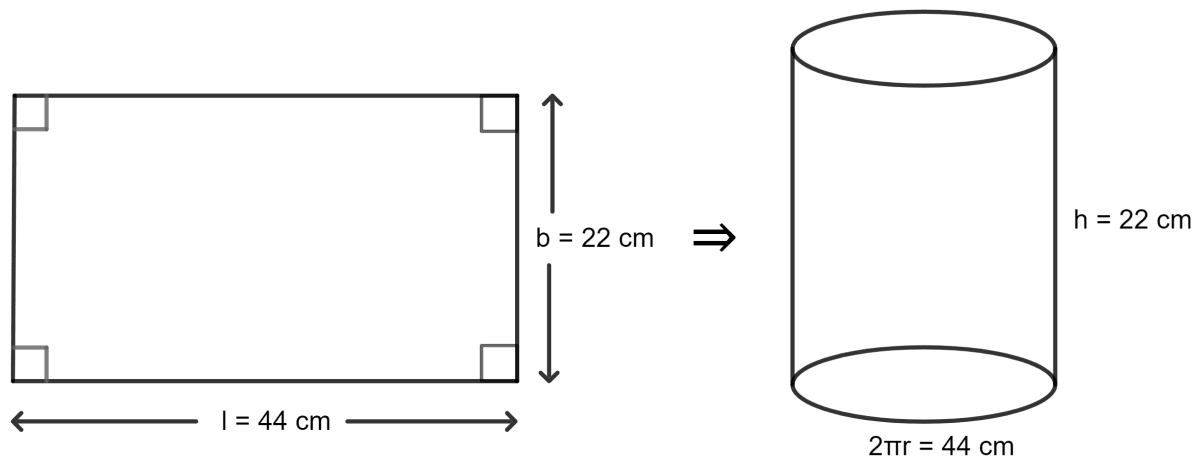
Also, height of the cylinder formed = Breadth of the sheet

⇒ h = 22 cm

Volume of the cylinder formed = πr²h

$= \dfrac{22}{7} \times 7^2 \times 22\\[1em] = \dfrac{22}{\cancel{7}} \times \cancel{7} \times 7 \times 22\\[1em] = 22 \times 7 \times 22\\[1em] = 3,388 cm^3$

Hence, the volume of the cylinder is 3,388 cm³.