Mathematics
Assertion (A): The line 3x + 3y + 5 = 0 crosses the x-axis at the point .
Reason (R): The ordinate of every point on x - axis is zero.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Straight Line Eq
1 Like
Answer
We know that,
The ordinate (y-coordinate) of every point on x-axis is zero.
So, reason (R) is true.
Substituting y = 0, in the equation of line 3x + 3y + 5 = 0, we get :
⇒ 3x + 3 x 0 + 5 = 0
⇒ 3x + 5 = 0
⇒ x =
Point of intersection =
So, assertion (A) is false.
Thus, Assertion (A) is false, Reason (R) is true.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
Given below are the equation of two lines:
y = 2x + 8 and y =
Assertion (A): The two lines are perpendicular to each other.
Reason (R): Their slopes are reciprocal of each other.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
l and m are two lines in the figure given below:
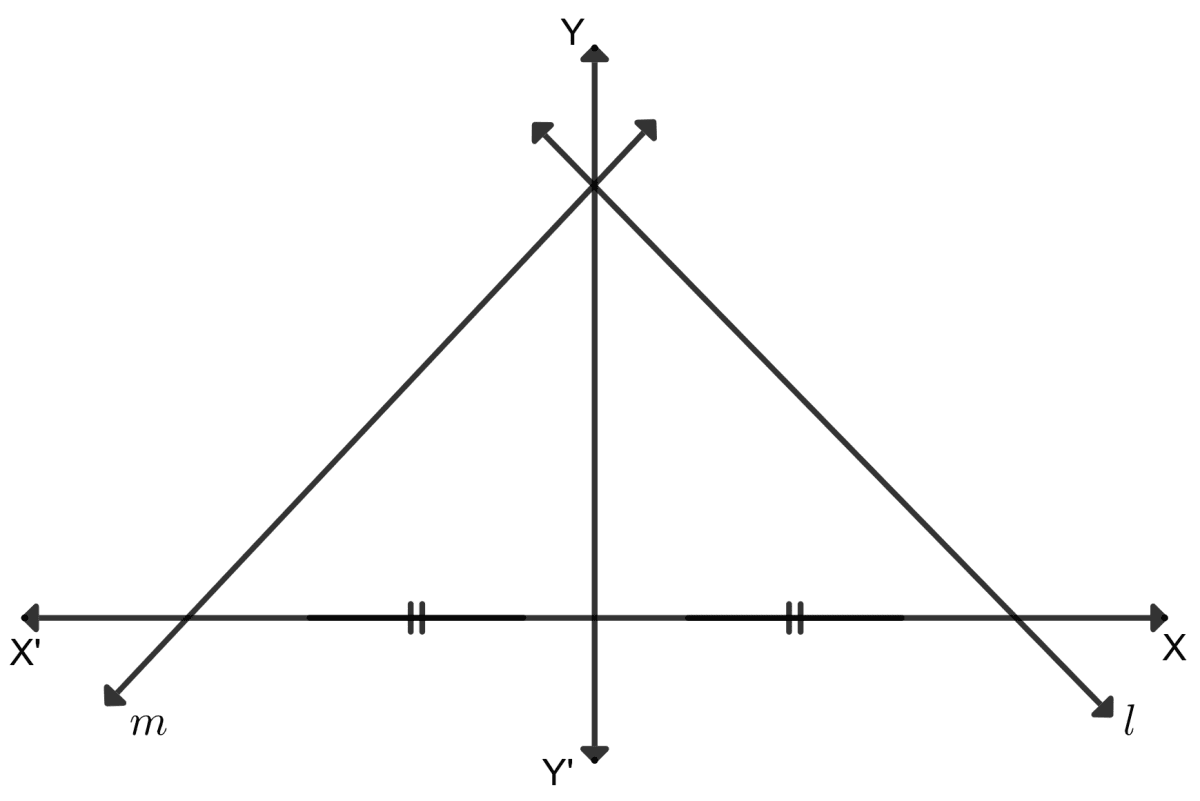
Assertion (A): They have equal y-intercept.
Reason (R): Their inclination is same.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Find the equation of a line whose inclination is 60° and y-intercept is -4.
Write down the gradient and the intercept on the y-axis of the line 3y + 2x = 12.