Mathematics
Case Study III
Tanusha went to a bank to withdraw money. She asked the cashier to give her ₹ 100 and ₹ 500 rupee notes only. The cashier agreed. Tanusha got x, ₹ 100-rupee notes and y, 500-rupee notes.
Based on this information, answer the following questions.
If Tanusha withdrew ₹ 15,000, then the above information can be represented by the linear equation:
(a) x + 5y = 150
(b) 5x + y = 150
(c) x + 5y + 150 = 0
(d) x + y = 150If she got 54 notes in all, then the above information can be represented by the linear equation:
(a) 100x + 500y = 54
(b) x + y = 54
(c) 500x + 100y = 54
(d) 100x + y = 54If Tanusha withdraws ₹16 000, then which combination of notes might she get?
(a) ₹500 notes = 30, ₹100 notes = 20
(b) ₹500 notes = 25, ₹100 notes = 25
(c) ₹500 notes = 20, ₹100 notes = 30
(d) ₹500 notes = 30, ₹100 notes = 10If she gets twenty 500-rupee notes and twenty-five 100-rupee notes, then the amount she withdraws is:
(a) ₹10,000
(b) ₹11,000
(c) ₹12,000
(d) ₹12,500Can Tanusha withdraw ₹10,050 under the given conditions?
(a) yes
(b) no
(c) can’t say anything
(d) none of these
Linear Equations
1 Like
Answer
1. Tanusha got x, ₹ 100-rupee notes and y, 500-rupee notes and withdraws ₹ 15,000.
⇒ 100x + 500y = 15000
⇒ 100(x + 5y) = 15000
⇒ x + 5y =
⇒ x + 5y = 150.
Hence, Option (a) is the correct option.
2. If she received x number ₹ 100 notes and y number of ₹ 500 notes and total notes are 54.
⇒ x + y = 54
Hence, Option (b) is the correct option.
3. If she withdaws ₹ 16,000 and gets x, ₹ 100 notes and y, 500 notes then.
⇒ 100x + 500y = 16000
⇒ 100(x + 5y) = 16000
⇒ x + 5y =
⇒ x + 5y = 160.
Substituting y = 30 and x = 10 in L.H.S. of the above equation, we get :
⇒ 10 + 5(30) = 10 + 150 = 160 = R.H.S.
Thus, no. of ₹ 100 notes = 10 and no. of ₹ 500 notes = 30.
Hence, Option (d) is the correct option.
4. Given,
She received 25 number ₹ 100 notes and 20 number of ₹ 500 notes,
Amount withdrawn = 100 × 25 + 500 × 20
= 2,500 + 10,000
= ₹ 12,500.
Hence, Option (d) is the correct option.
5. Let x be the number of ₹100 notes and y be the number of ₹500 notes.
The total amount is 100x + 500y.
Can Tanusha withdraw ₹ 10,050.
This means we need to check if the equation 100x + 500y = 10050 has integer solutions for x and y.
The value of x ₹100 notes is 100x, which is a multiple of 100.
The value of y ₹500 notes is 500y, which is also a multiple of 100.
The sum of these two values, the total amount withdrawn, must also be a multiple of 100.
Since, ₹ 10,050 is not a multiple of 100.
Therefore, it is not possible to form the amount ₹ 10,050 using only ₹ 100 and ₹ 500 notes.
Hence, Option (b) is the correct option.
Answered By
1 Like
Related Questions
Case Study I Ritesh bought a new well-furnished two-bedroom flat in a society. The layout of the flat is shown in the figure alongside. The builder claims that the areas of the two bedrooms and the kitchen together is 95 square metres. All the dimensions in the figure are in metre (m).
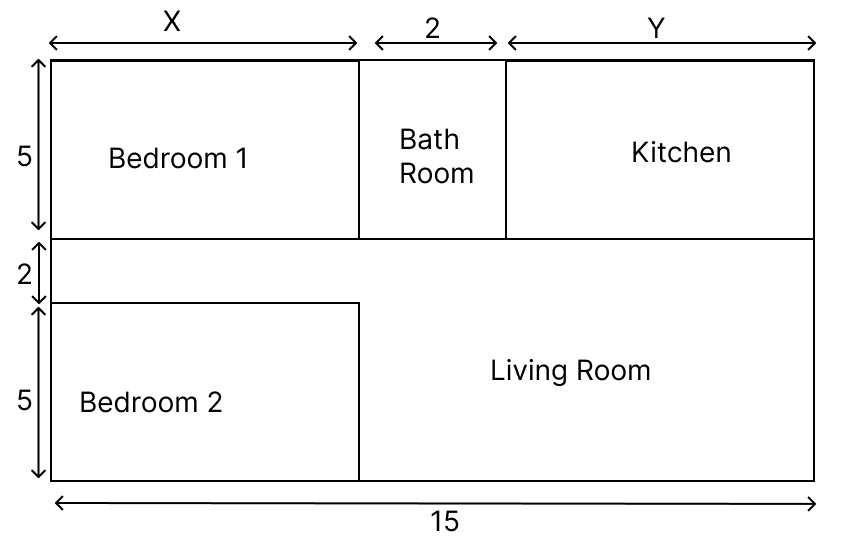
Study the above information and answer the following questions.
Which of the following pair of linear equations represent the given situation?
(a) x + y = 19, 2x + y = 13
(b) x + y = 13, 2x + y = 19
(c) x − y = 19, 2x − y = 13
(d) x + y = 13, 2x − y = 19The perimeter of the outer boundary of the layout is:
(a) 54 m
(b) 27 m
(c) 50 m
(d) 52 mTotal area of bedroom 1 and kitchen is:
(a) 60 m2
(b) 70 m2
(c) 65 m2
(d) 95 m2The area of the living room is:
(a) 50 m2
(b) 60 m2
(c) 70 m2
(d) 75 m2The cost of laying tiles on the floor of the kitchen at the rate of ₹200 per sq m is:
(a) ₹ 7,000
(b) ₹ 6,000
(c) ₹ 5,200
(d) ₹ 5,000
Case Study II
There are two mobile-phone companies – P and Q, that offer different plans. Company P charges a monthly fee of ₹ 40 plus ₹ 0.5 per minute of talk time. Company Q charges a monthly service fee of ₹ 30 plus ₹ 1 per minute of talk time.
Based on this information answer the following questions:
The linear equation which expresses the plan of company P is :
(a) y = 0.5x + 40
(b) y = 40x + 0.5
(c) y = x + 40.5
(d) y = 40 − 0.5xThe linear equation which expresses the plan of company Q is:
(a) y = 30x + 1
(b) y = x + 30
(c) y = x − 30
(d) y = 30x − 1How many minutes of talk time would yield equal expenditure from both companies?
(a) 10 minutes
(b) 15 minutes
(c) 20 minutes
(d) 25 minutesManisha took the plan of company P and used 400 minutes of talk time. She spent:
(a) ₹240
(b) ₹430
(c) ₹220
(d) ₹215If in a month, Anurag wants to use only 300 minutes of talk time, then which company’s plan is better for him?
(a) Company P
(b) Company Q
(c) Both offer the same plan
(d) Can’t be determined
Assertion(A): If 8x + 7y = 37 and 7x + 8y = 38, then x = -2, y = 3.
Reason(R): ax + by = c and bx + ay = d is not simultaneous linear equations in two variables.
A is true, R is false
A is false, R is true
Both A and R are true
Both A and R are false
Assertion(A): is a pair of simultaneous linear equations.
Reason(R): An equation of the form ax + by + c = 0, a ≠ 0, b ≠ 0 is called linear equations in two variables.
A is true, R is false
A is false, R is true
Both A and R are true
Both A and R are false