Mathematics
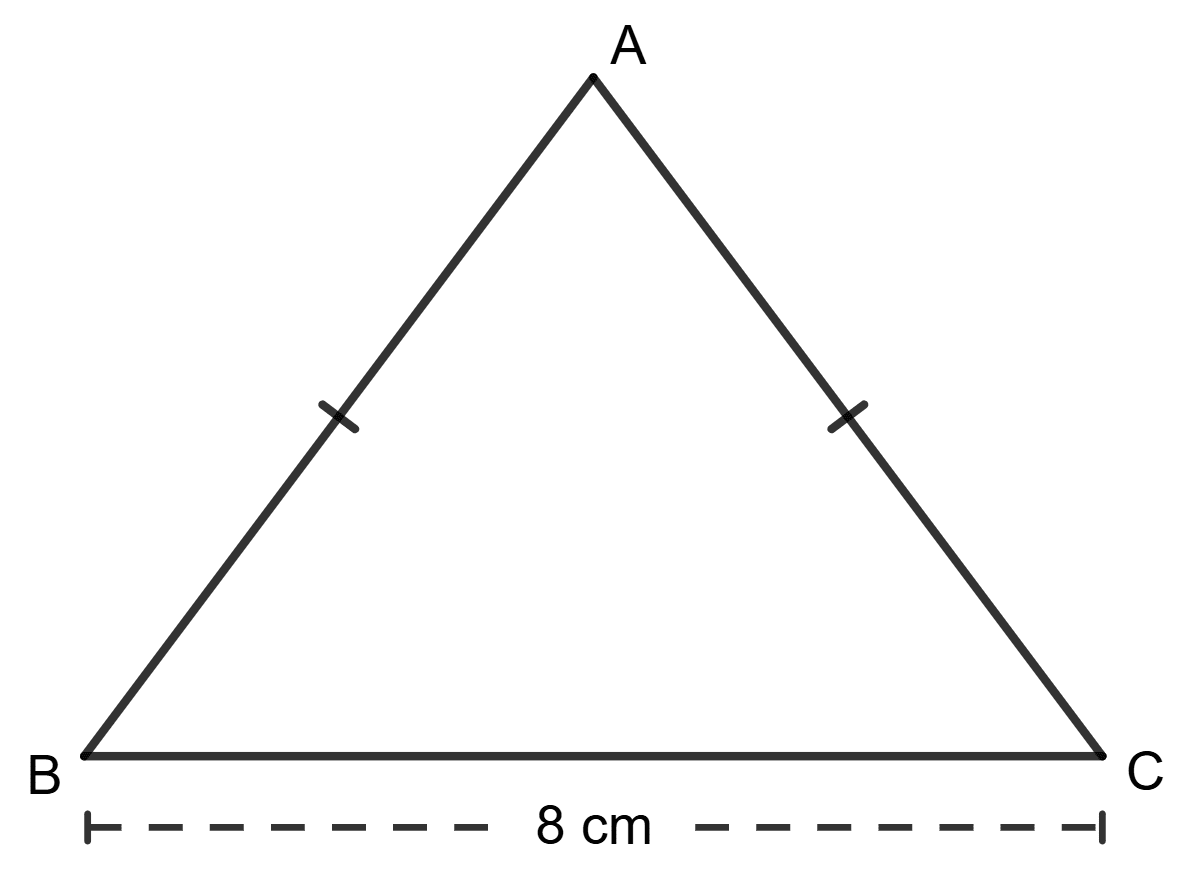
In the figure, given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find :
(i) sin B
(ii) tan C.
(iii) sin2 B + cos2 B
(iv) tan C - cot B
Trigonometric Identities
14 Likes
Answer
In isosceles Δ ABC, the perpendicular drawn from angle A to the side BC divides BC into 2 equal parts.
BD = DC = = 4
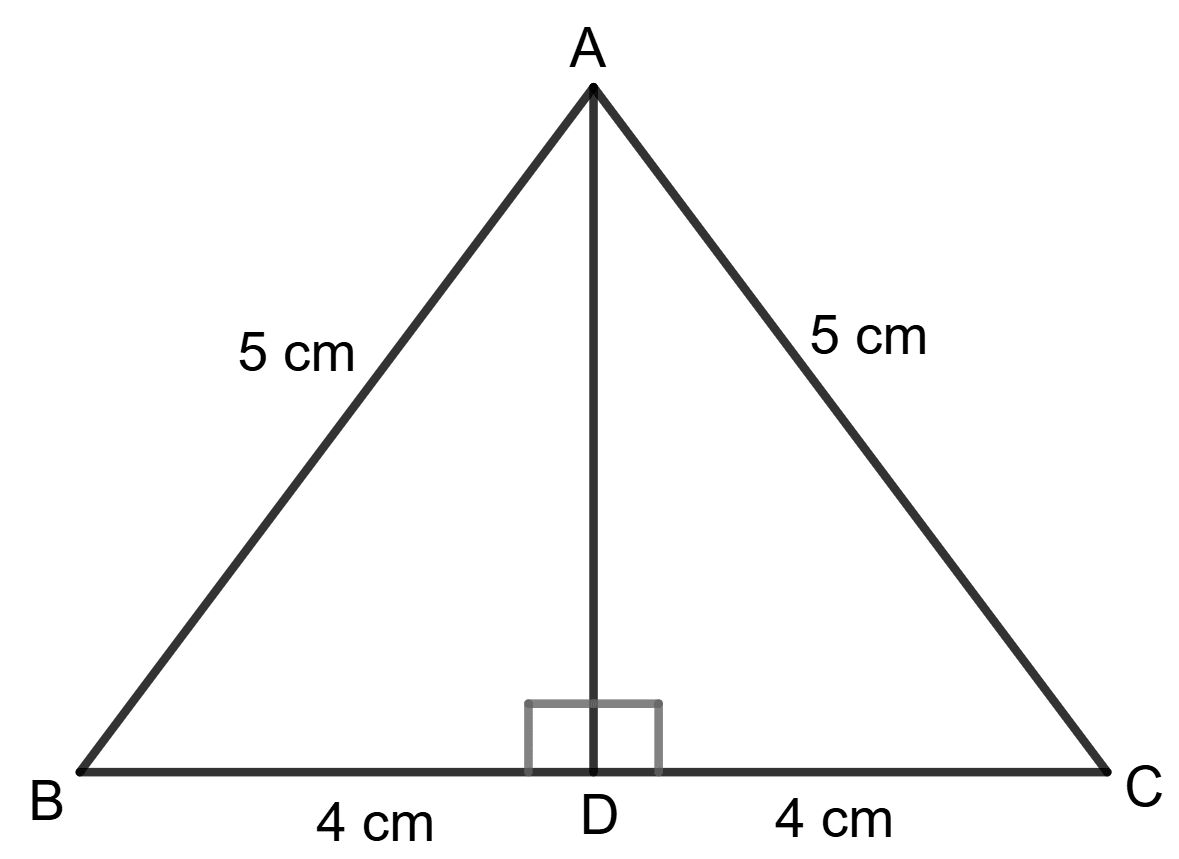
In Δ ABD,
⇒ AB2 = BD2 + AD2 (∵ AB is hypotenuse)
⇒ 52 = 42 + AD2
⇒ 25 = 16 + AD2
⇒ AD2 = 25 - 16
⇒ AD2 = 9
⇒ AD =
⇒ AD = 3
(i) sin B =
Hence, sin B =
(ii) tan C =
Hence, tan C =
(iii) sin2 B + cos2 B
sin B =
cos B =
Now, sin2 B + cos2 B
Hence, sin2 B + cos2 B = 1.
(iv) tan C - cot B
tan C =
cot B =
Now, tan C - cot B
Hence, tan C - cot B = .
Answered By
7 Likes
Related Questions
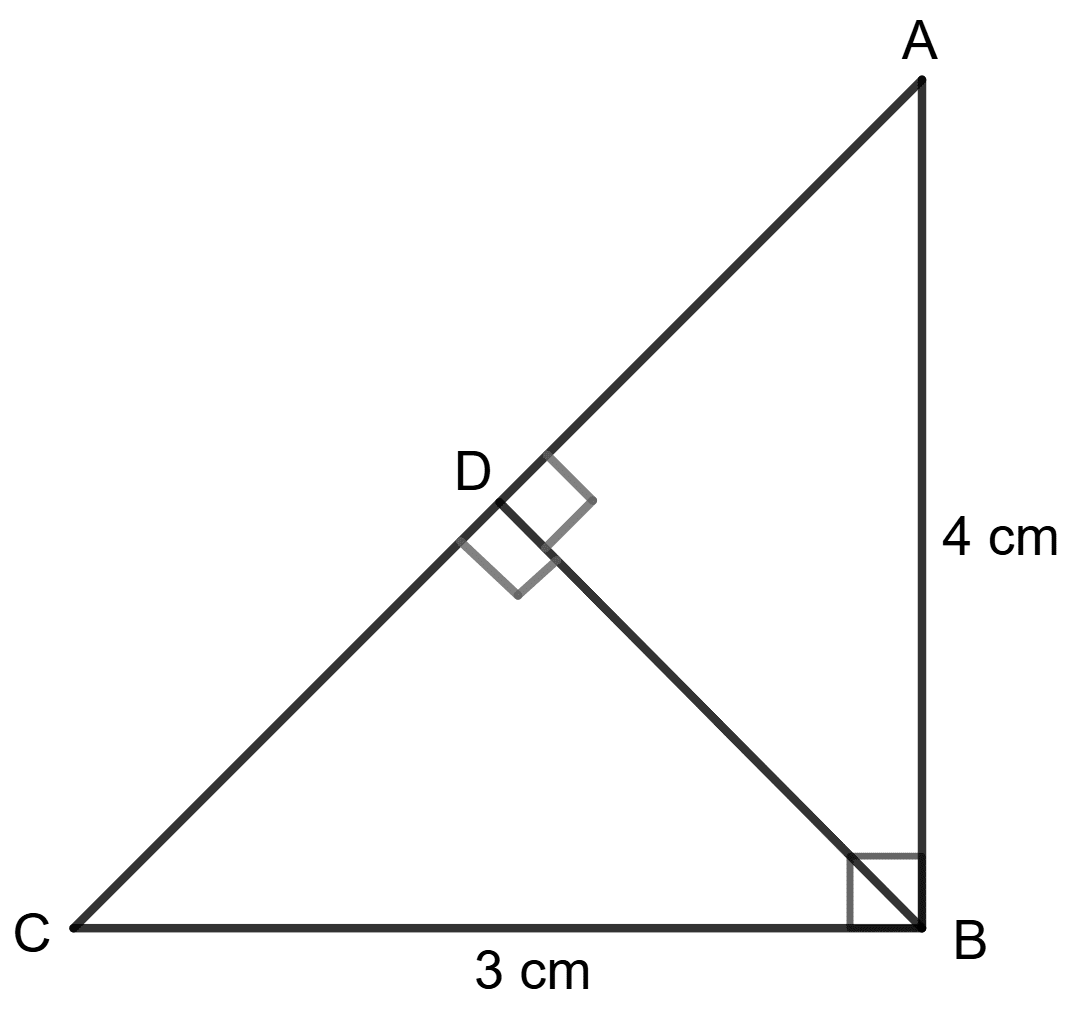
In the given figure, triangle ABC is right-angled at B. D is the foot of the perpendicular from B to AC. Given that BC = 3 cm and AB = 4 cm. Find :
(i) tan ∠DBC
(ii) sin ∠DBA
In triangle ABC, AB = AC = 15 cm and BC = 18 cm, find cos ∠ABC.
In triangle ABC; ∠ABC = 90°, ∠CAB = x°, and BC = 15 cm. Find the measures of AB and AC.
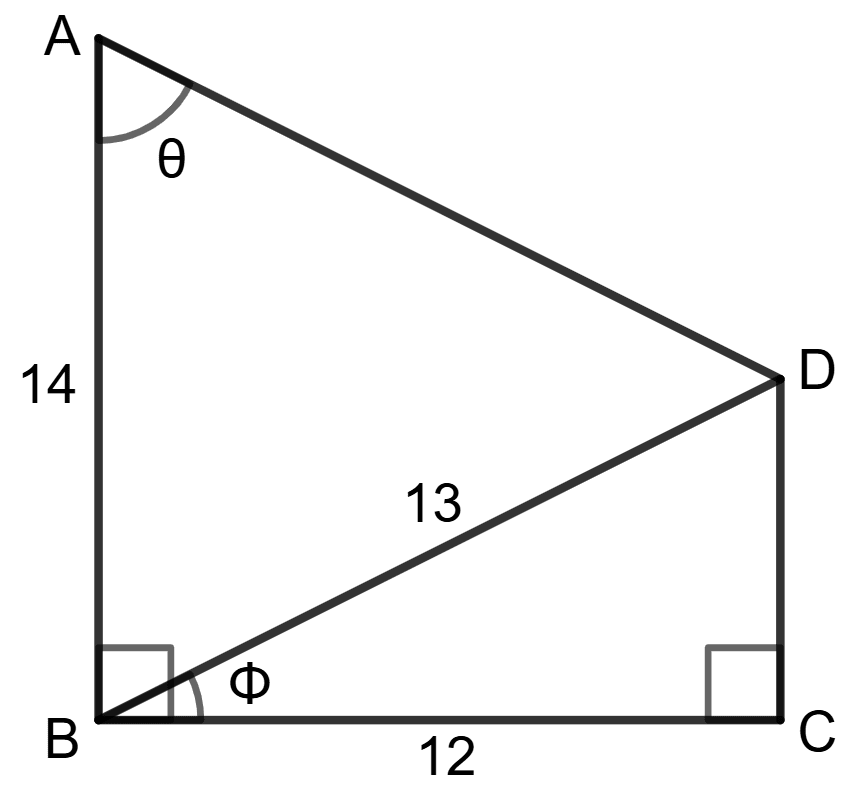
Using the measurements given in the following figure :
(i) Find the value of sin Φ and tan θ.
(ii) Write an expression for AD in terms of θ.