Mathematics
Find the equation of the line perpendicular to the line joining the points A(1, 2) and B(6, 7) and passing through the point which divides the line segment AB in the ratio 3 : 2.
Straight Line Eq
36 Likes
Answer
Let the slope of line joining A(1, 2) and B(6, 7) be s1. Slope of two points is given by,
Let slope of perpendicular line be s2. So,
Given, the new line passes through the point which divides the line segment AB in the ratio 3 : 2. By section formula coordinates are,
Equation of the line having slope -1 and passing through (4, 5) can be given by point-slope form i.e.,
Hence, the equation of the required line is x + y - 9 = 0.
Answered By
19 Likes
Related Questions
Write down the equation of a line parallel to x - 2y + 8 = 0 and passing through the point (1, 2).
Write down the equation of the line passing through (-3, 2) and perpendicular to the line 3y = 5 - x.
The points A(7, 3) and C(0, -4) are two opposite vertices of a rhombus ABCD. Find the equation of the diagonal BD.
A and B are two points on the x-axis and y-axis respectively.
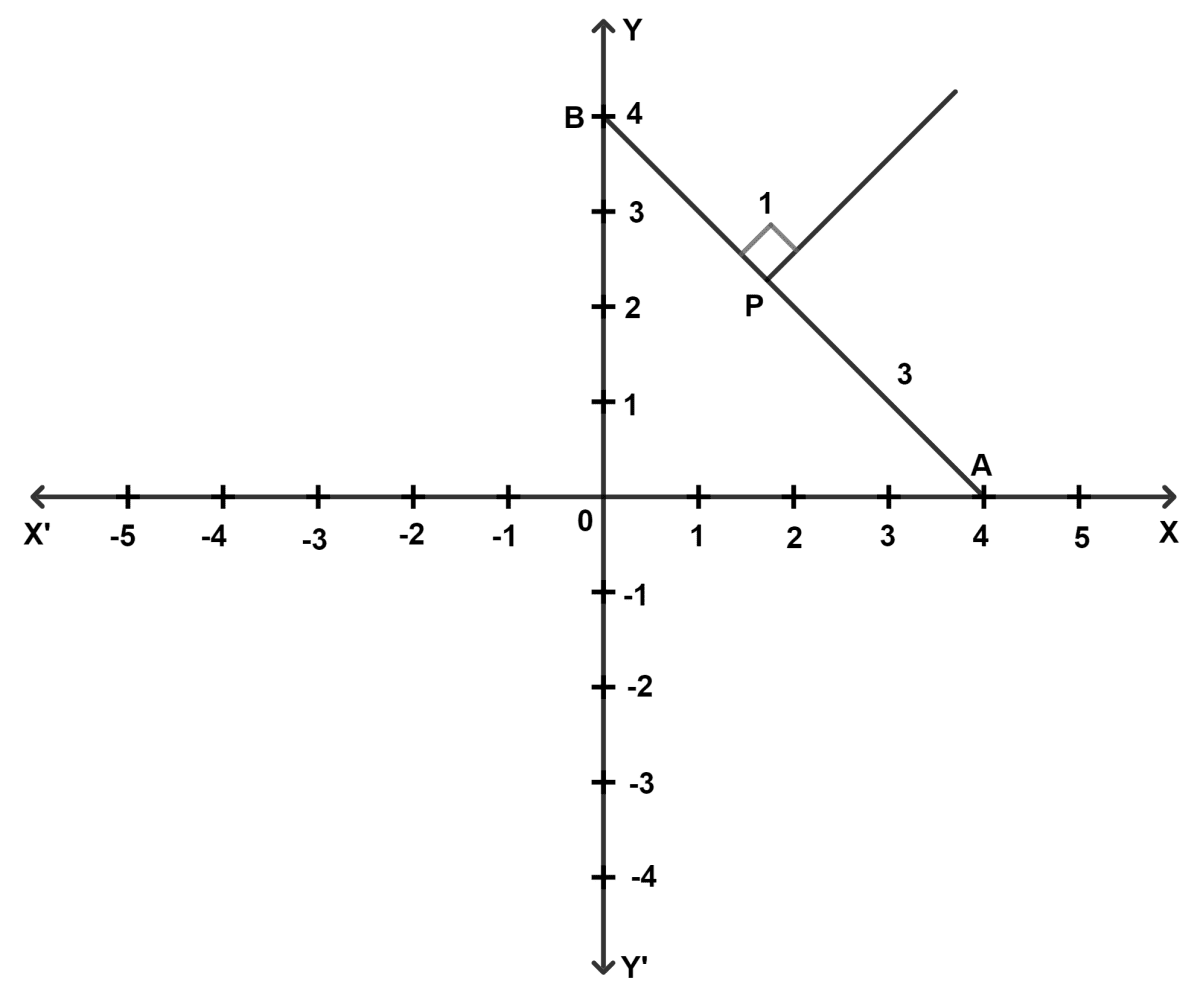
(a) Write down the co-ordinates of A and B.
(b) P is a point on AB such that AP : PB = 3 : 1. Using section formula find the coordinates of point P.
(c) Find the equation of a line passing through P and perpendicular to AB.