Mathematics
Find which of the following points lie on the line x - 2y + 5 = 0 :
(i) (1, 3)
(ii) (0, 5)
(iii) (-5, 0)
(iv) (5, 5)
(v) (2, -1.5)
(vi) (-2, -1.5)
Straight Line Eq
13 Likes
Answer
(i) Substituting x = 1 and y = 3 in the L.H.S. of the equation x - 2y + 5 = 0, we get :
L.H.S. = 1 - 2 × 3 + 5
= 1 - 6 + 5
= -5 + 5
= 0.
Since, L.H.S. = R.H.S.
∴ Point (1, 3) satisfies the equation.
Hence, (1, 3) lies on the line represented by the equation x - 2y + 5 = 0.
(ii) Substituting x = 0 and y = 5 in the L.H.S. of the equation x - 2y + 5 = 0, we get :
L.H.S. = 0 - 2 × 5 + 5
= 0 - 10 + 5
= -5
Since, L.H.S. ≠ R.H.S.
∴ Point (0, 5) does not satisfies the equation.
Hence, (0, 5) does not lies on the line represented by the equation x - 2y + 5 = 0.
(iii) Substituting x = -5 and y = 0 in the L.H.S. of the equation x - 2y + 5 = 0, we get :
L.H.S. = -5 - 2 × 0 + 5
= -5 - 0 + 5
= -5 + 5
= 0.
Since, L.H.S. = R.H.S.
∴ Point (-5, 0) satisfies the equation.
Hence, (-5, 0) lies on the line represented by the equation x - 2y + 5 = 0.
(iv) Substituting x = 5 and y = 5 in the L.H.S. of the equation x - 2y + 5 = 0, we get :
L.H.S. = 5 - 2 × 5 + 5
= 5 - 10 + 5
= 10 - 10
= 0.
Since, L.H.S. = R.H.S.
∴ Point (5, 5) satisfies the equation.
Hence, (5, 5) lies on the line represented by the equation x - 2y + 5 = 0.
(v) Substituting x = 2 and y = -1.5 in the L.H.S. of the equation x - 2y + 5 = 0, we get :
L.H.S. = 2 - 2 × (-1.5) + 5
= 2 + 3 + 5
= 10
Since, L.H.S. ≠ R.H.S.
∴ Point (2, -1.5) does not satisfies the equation.
Hence, (2, -1.5) does not lies on the line represented by the equation x - 2y + 5 = 0.
(vi) Substituting x = -2 and y = -1.5 in the L.H.S. of the equation x - 2y + 5 = 0, we get :
L.H.S. = -2 - 2 × (-1.5) + 5
= -2 + 3 + 5
= 6
Since, L.H.S. ≠ R.H.S.
∴ Point (-2, -1.5) does not satisfies the equation.
Hence, (-2, -1.5) does not lies on the line represented by the equation x - 2y + 5 = 0.
Answered By
5 Likes
Related Questions
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find :
(i) equation of line AB.
(ii) equation of line CD.
(iii) co-ordinates of point E and D.

Find the equation of the line through the points A(-1, 3) and B(0, 2). Hence, show that the points A, B and C(1, 1) are collinear.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
(i) Write the co-ordinates of A.
(ii) Find the length of AB and AC.
(iii) Find the ratio in which Q divides AC.
(iv) Find the equation of the line AC.
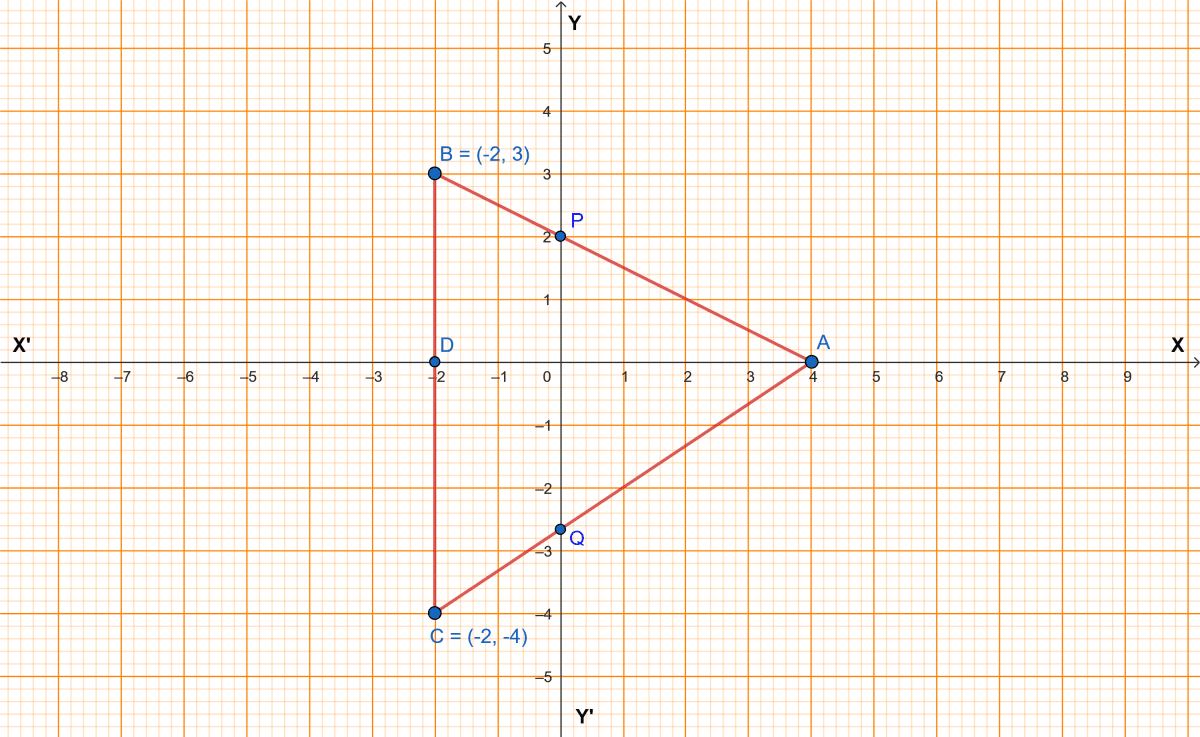
A line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ratio 1 : 2.
(i) Find the co-ordinates of A and B.
(ii) Find the equation of the line through P and perpendicular to AB.
