Mathematics
In the given figure, PQR is a triangle whose area is 75 cm2. S and T are mid-points of sides PQ and PR respectively. Calculate the area of quadrilateral SQRT.
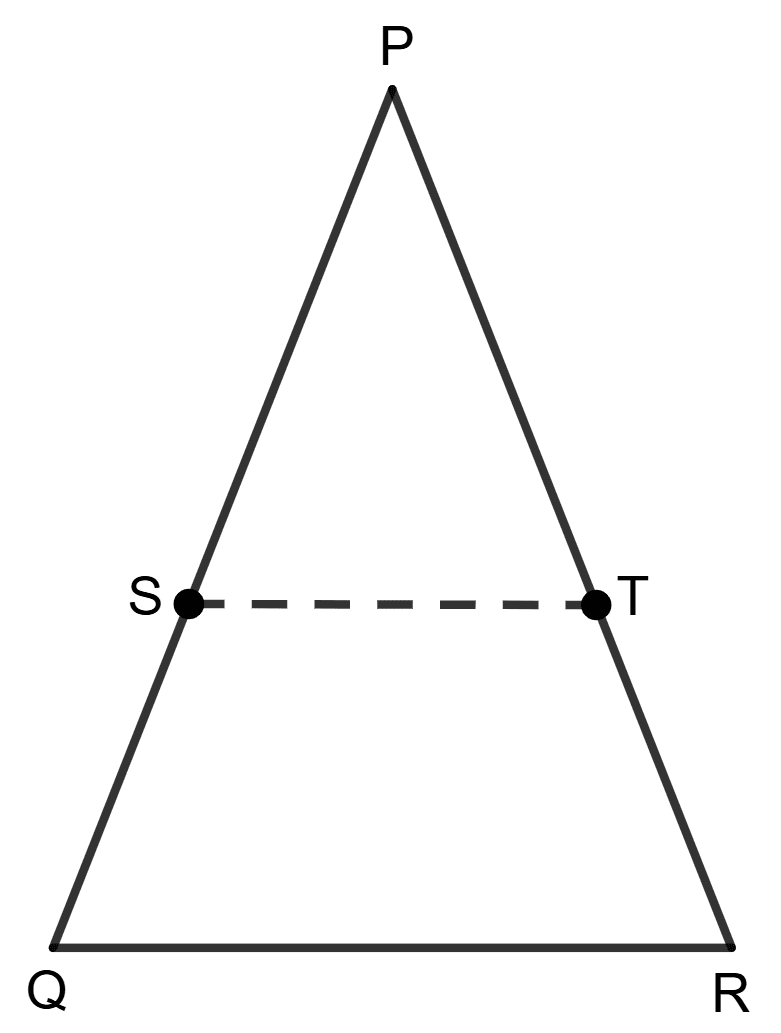
Mid-point Theorem
3 Likes
Answer
56.25 cm2
Reason
Using midpoint theorem, which states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and is half the length of the third side.
Given,
S and T are the midpoints of PQ and PR.
ST || QR and ST =
Draw PM perpendicular to QR. Let PM meets ST at N.
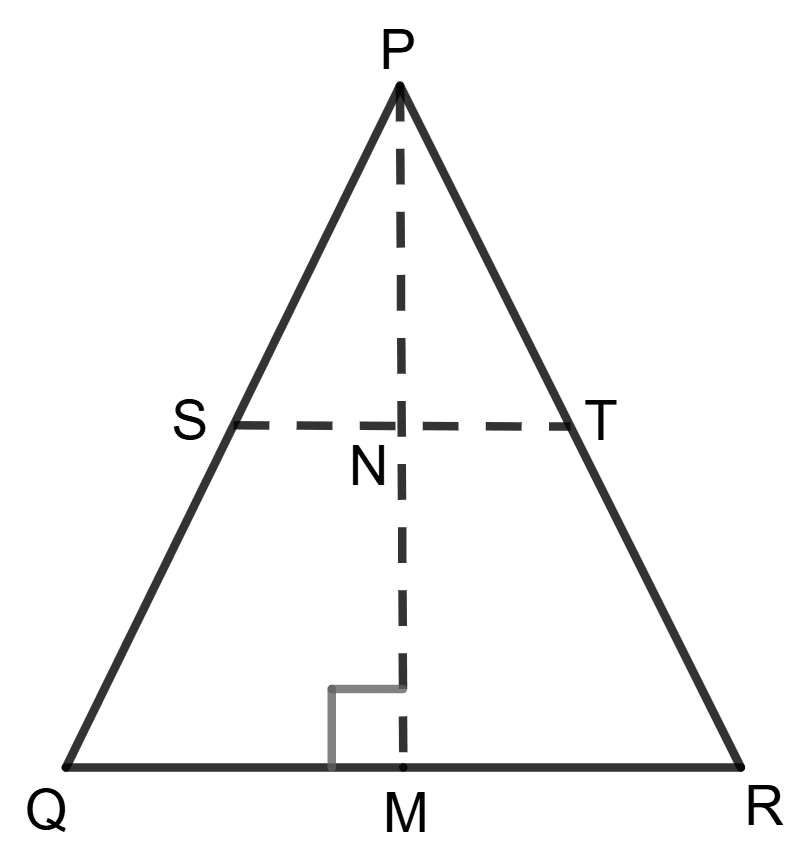
As, ST || QR
∴ ∠SNP = ∠QMN = 90°
As, S is mid-point of PQ and SN || QM,
∴ N is mid-point of PM.
Area of triangle =
Area of trapezium STRQ = Area of △PQR - Area of △PST = 75 - 18.75 = 56.25 cm2.
Answered By
3 Likes
Related Questions
Assertion (A): Using the information in the given figure, we have PQ = 10 cm.
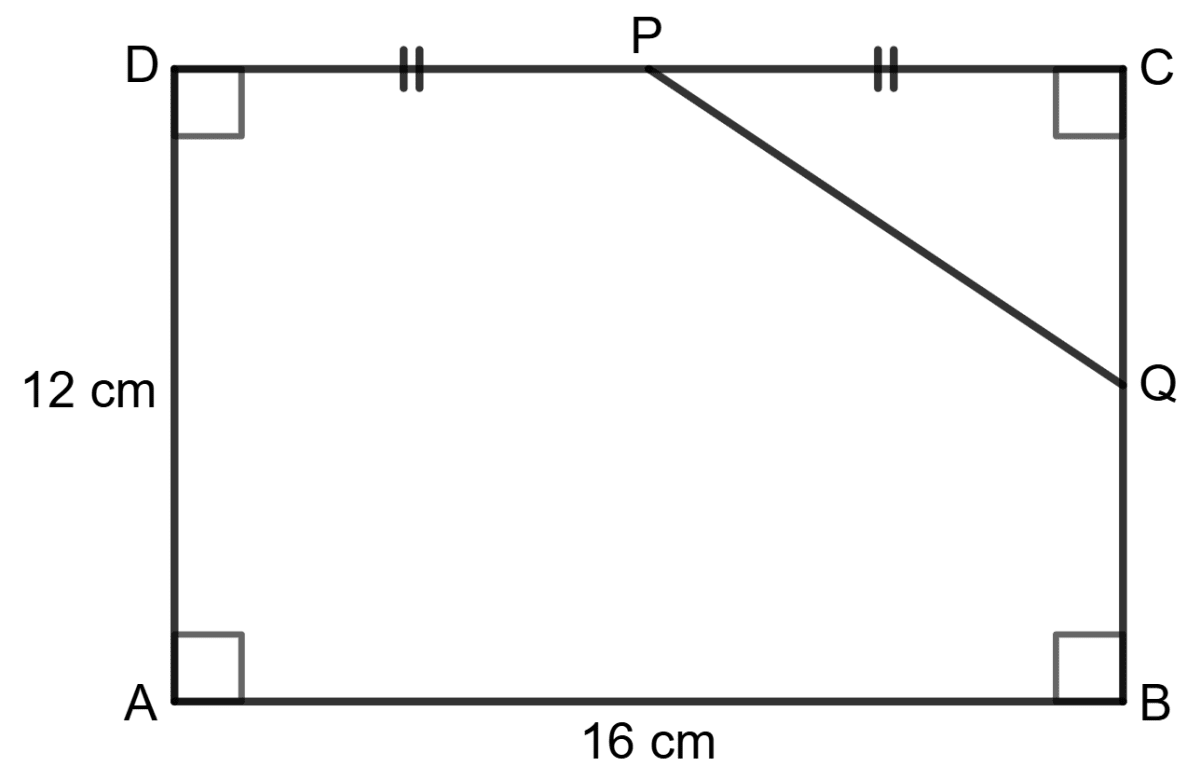
Reason (R): In right-triangle DAB, DB = 20 cm.

- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
P is the mid-point of the hypotenuse AB of the right-angled triangle ABC. Prove that : AB = 2 CP.