Mathematics
Given a line segment AB joining the points A(-4, 6) and B(8, 3). Find :
(i) the ratio in which line segment AB is divided by y-axis.
(ii) the co-ordinates of the point of intersection.
(iii) equation of perpendicular bisector of AB.
Section Formula
8 Likes
Answer
(i) Let the y-axis divide AB in the ratio m1 : m2.
By section-formula, the x-coordinate =
Since, the x-coordinate on y-axis is 0. Putting value in above formula we get :
Hence, required ratio = 1 : 2.
(ii) The x-coordinate equals to zero on y-axis.
By section formula, the y-coordinate =
Substituting value in above formula, we get :
Hence, the coordinates of the point of intersection are (0, 5).
(iii) By formula,
Mid-point =
Let M be the mid-point of AB.
M = .
Slope of AB =
We know that,
Product of slope of perpendicular lines = -1.
Let slope of perpendicular bisector be h.
∴ h × = -1
⇒ h = 4.
By point-slope form,
Equation : y - y1 = m(x - x1)
⇒ y - = 4(x - 2)
⇒ = 4(x - 2)
⇒ 2y - 9 = 8(x - 2)
⇒ 2y - 9 = 8x - 16
⇒ 2y - 8x - 9 + 16 = 0
⇒ 2y - 8x + 7 = 0
⇒ 8x - 2y = 7.
Hence, equation of perpendicular bisector of AB is 8x - 2y = 7.
Answered By
3 Likes
Related Questions
Solve the following inequation and represent the solution set on a number line :
; x ∈ R.
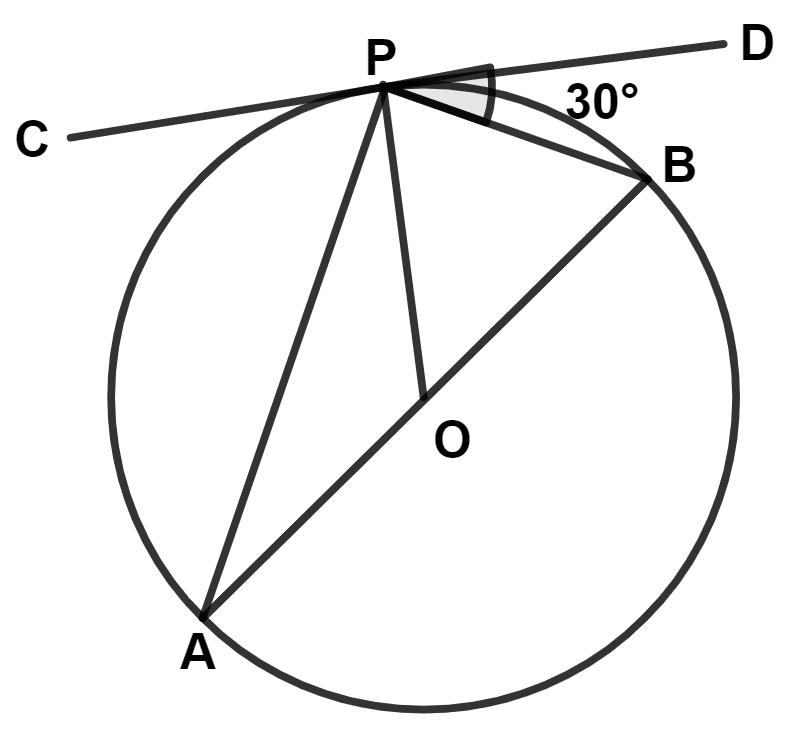
In the given figure, O is the center of the circle, AB is diameter and CPD is a tangent to the circle at P. If ∠BPD = 30°, find :
(i) ∠APC
(ii) ∠BOP
(iii) ∠OAP
If b is the mean proportion between a and c, prove that :
The denominator of a fraction is 1 more than its numerator. The sum of fraction and its reciprocal is , find the fraction.