Mathematics
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of :
(i) ∠OCA,
(ii) ∠OAC.

Circles
26 Likes
Answer
We know that,
Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
∴ ∠AOB = 2∠ACB
⇒ 70° = 2∠ACB
⇒ ∠ACB = = 35°.
(i) From figure,
∠OCA = ∠ACB = 35°.
Hence, ∠OCA = 35°.
(ii) Since, BC is a straight line,
∴ ∠AOB + ∠AOC = 180°
⇒ 70° + ∠AOC = 180°
⇒ ∠AOC = 180° - 70° = 110°.
In △OAC,
⇒ ∠OCA + ∠OAC + ∠AOC = 180°
⇒ ∠OAC + 35° + 110° = 180°
⇒ ∠OAC + 145° = 180°
⇒ ∠OAC = 180° - 145° = 35°.
Hence, ∠OAC = 35°.
Answered By
18 Likes
Related Questions
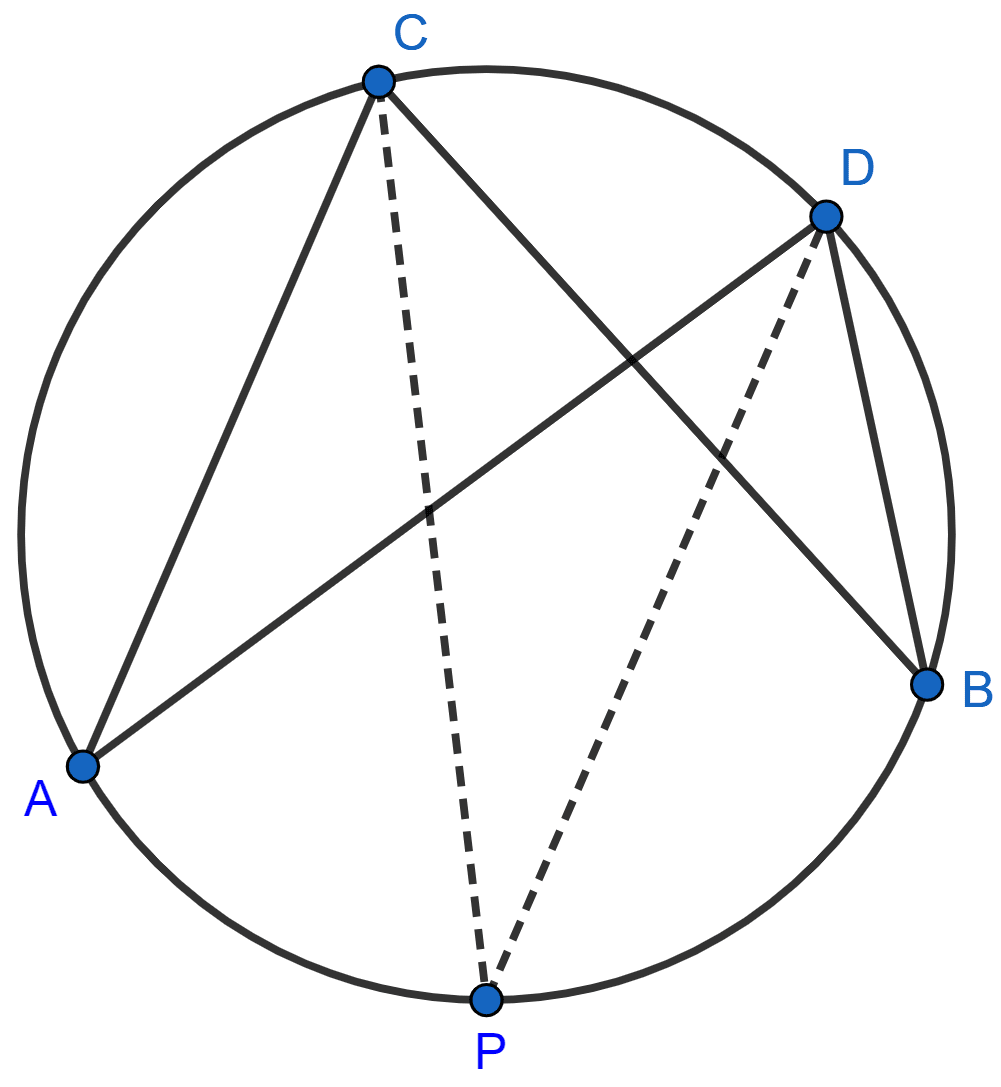
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED

In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD