If all the three altitudes of a triangle are equal, the triangle is equilateral. Prove it.

From figure,

ABC is the triangle. AD, BE and CF are the altitudes drawn on sides BC, CA and AB, such that AD = BE = CF = x (let).

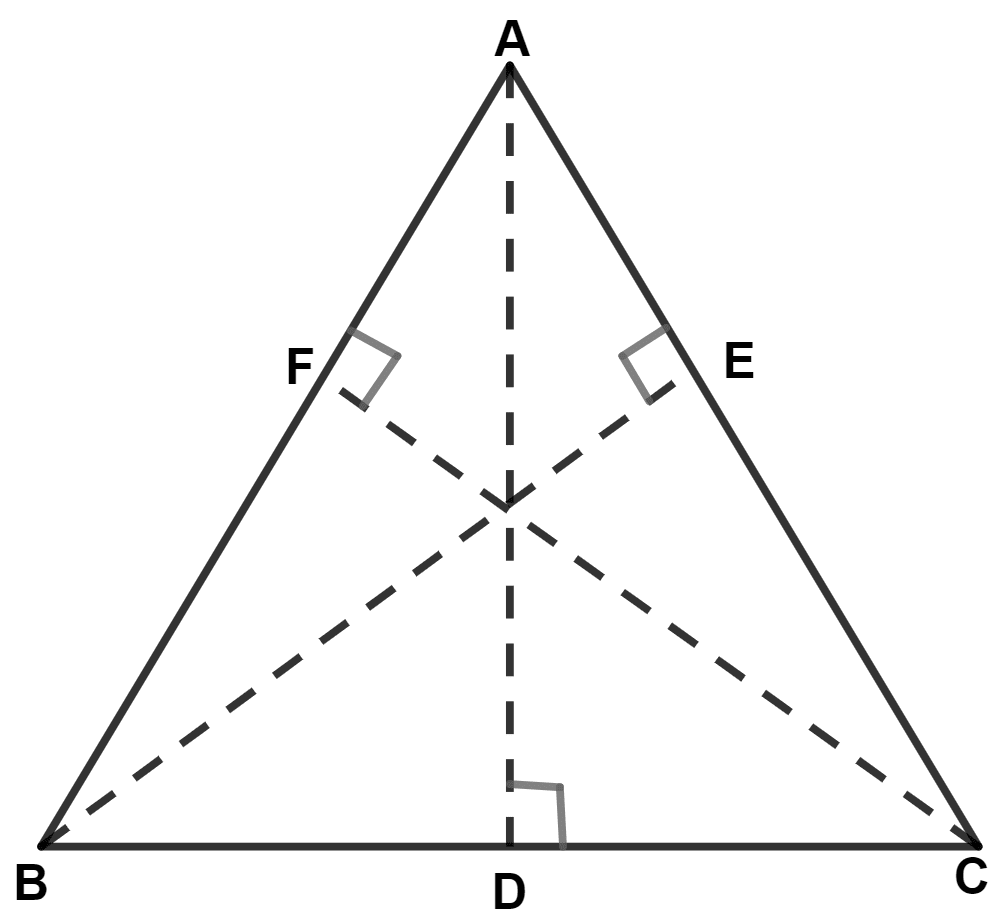
By formula,

Area of triangle = $\dfrac{1}{2}$ × base × height

∴ $\dfrac{1}{2} \times BC \times AD = \dfrac{1}{2} \times AB \times CF = \dfrac{1}{2} \times CA \times BE$

∴ BC × AD = AB × CF = CA × BE

⇒ BC.x = AB.x = CA.x

⇒ BC = AB = CA

Hence, Δ ABC is an equilateral triangle.

Hence, proved that if all the three altitudes of a triangle are equal, the triangle is equilateral.