Physics
The image of a candle flame placed at a distance of 36 cm from a spherical lens, is formed on a screen placed at a distance of 72 cm from the lens. Calculate the focal length of the lens and its power.
Refraction Lens
6 Likes
Answer
Given,
Object distance (u) = - 36 cm
As, image is formed on a screen then,
Image distance (v) = + 72 cm
Let, focal length be f.
From lens formula,
Now,
Answered By
3 Likes
Related Questions
How much heat is required to convert 500 g of ice at 0°C to water at 0°C? The latent heat of fusion of ice is 330 J g⁻¹.
Copy and complete the nuclear reaction by filling in the blanks.
Below is an incomplete table showing the arrangement of electromagnetic spectrum in the increasing order of their wavelength. Complete the table.
Gamma ray X – ray U V rays Visible rays Infrared A Radio waves (a) Identify the radiation A.
(b) Name the radiation used to detect fracture in bones.
(c) Name one property common to both A and Radio waves.
(a) Why do we use red colour as a danger signal on the top of a skyscraper?
(b) The diagram below shows the path of a blue ray through the prism :
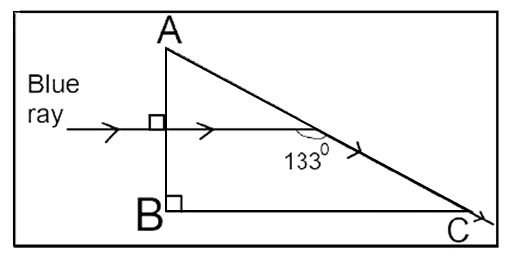
- Calculate the critical angle of the material of the prism for blue colour.
- What is the measure of the angle of this prism (A)?
- Which colour should replace the blue ray, for the ray to undergo Total Internal Reflection?