Mathematics
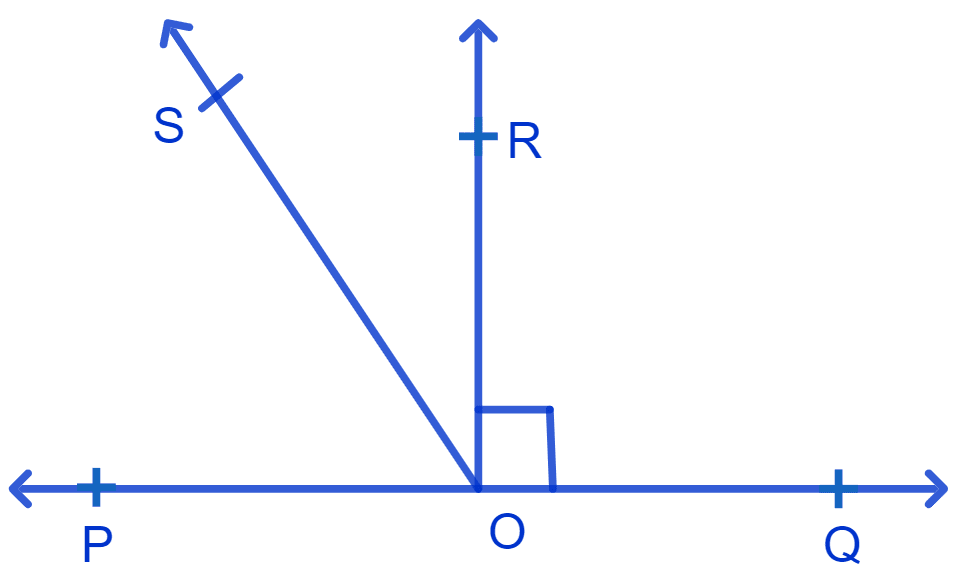
In Fig. POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that
∠ROS = (∠QOS – ∠POS).
Lines & Angles
12 Likes
Answer
Since, OR ⊥ PQ
∴ ∠ROP = 90° and ∠ROQ = 90°
∴ ∠ROS = 90° - ∠POS …….(1)
⇒ ∠QOS = ∠QOR + ∠ROS
⇒ ∠QOS = 90° + ∠ROS
⇒ 90° = ∠QOS - ∠ROS …..(2)
Substituting value of 90° from equation (2) in equation (1), we get :
⇒ ∠ROS = (∠QOS - ∠ROS) - ∠POS
⇒ ∠ROS + ∠ROS = ∠QOS - ∠POS
⇒ 2(∠ROS) = ∠QOS - ∠POS
⇒ ∠ROS = (∠QOS - ∠POS)
Hence, proved ∠ROS = (∠QOS - ∠POS).
Answered By
7 Likes
Related Questions
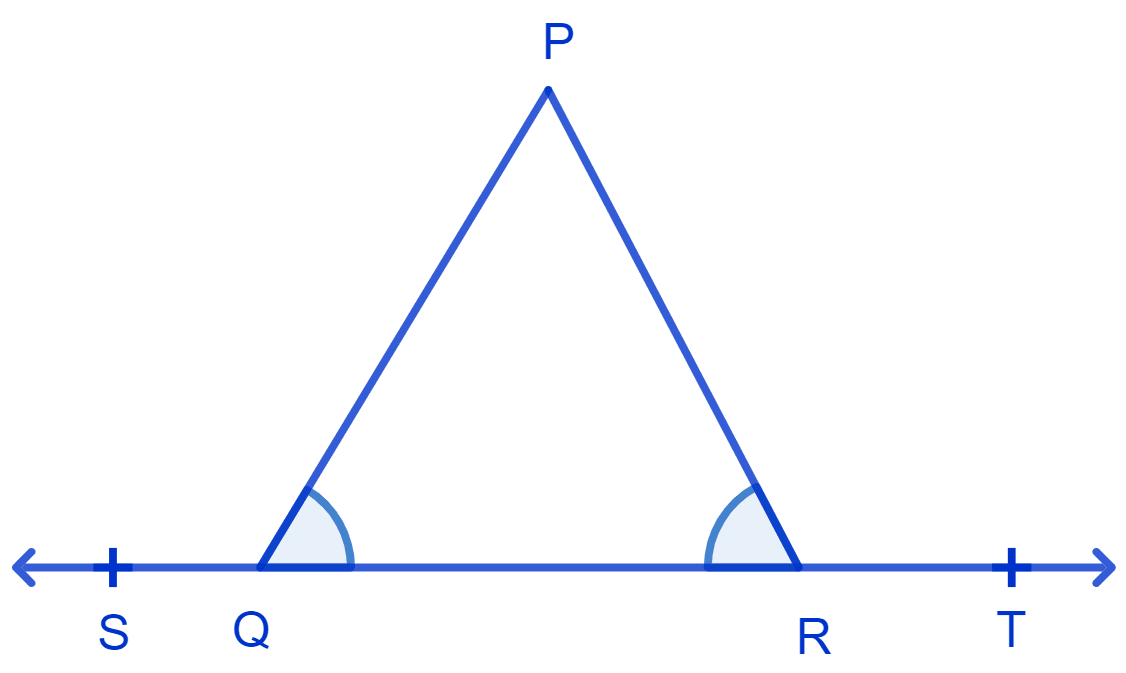
In Fig. ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
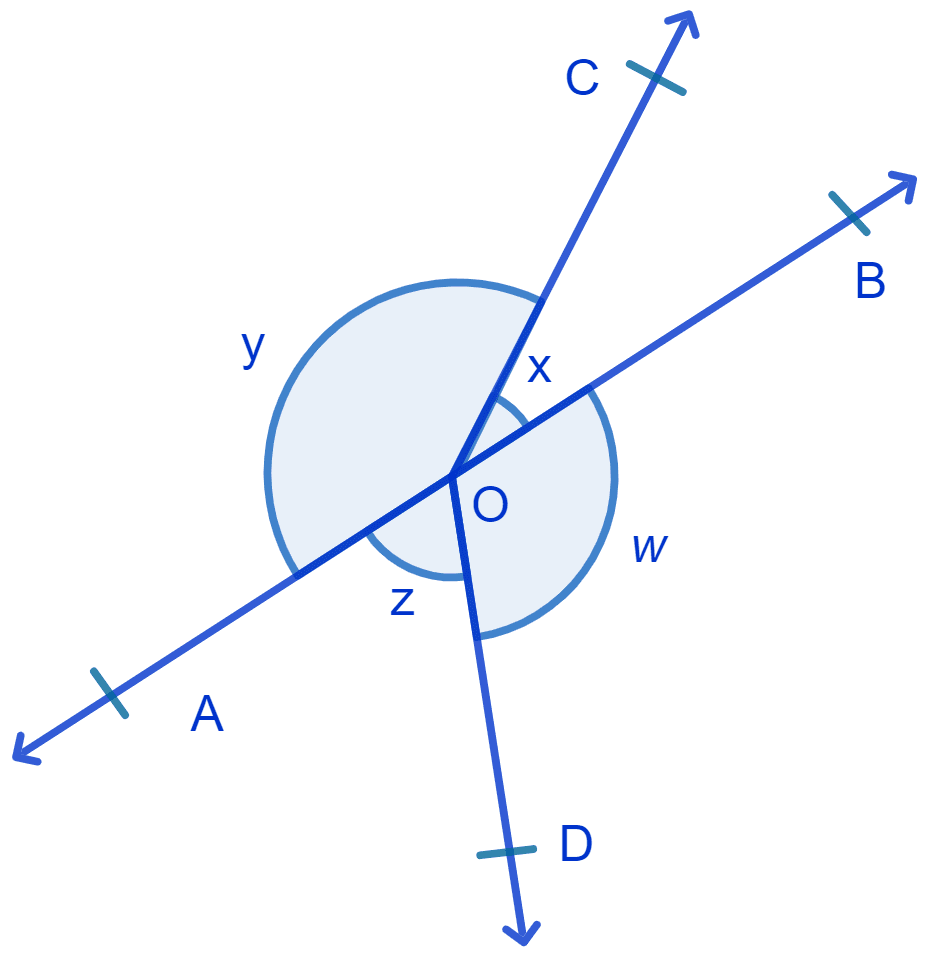
In Fig. if x + y = w + z, then prove that AOB is a line.
It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.
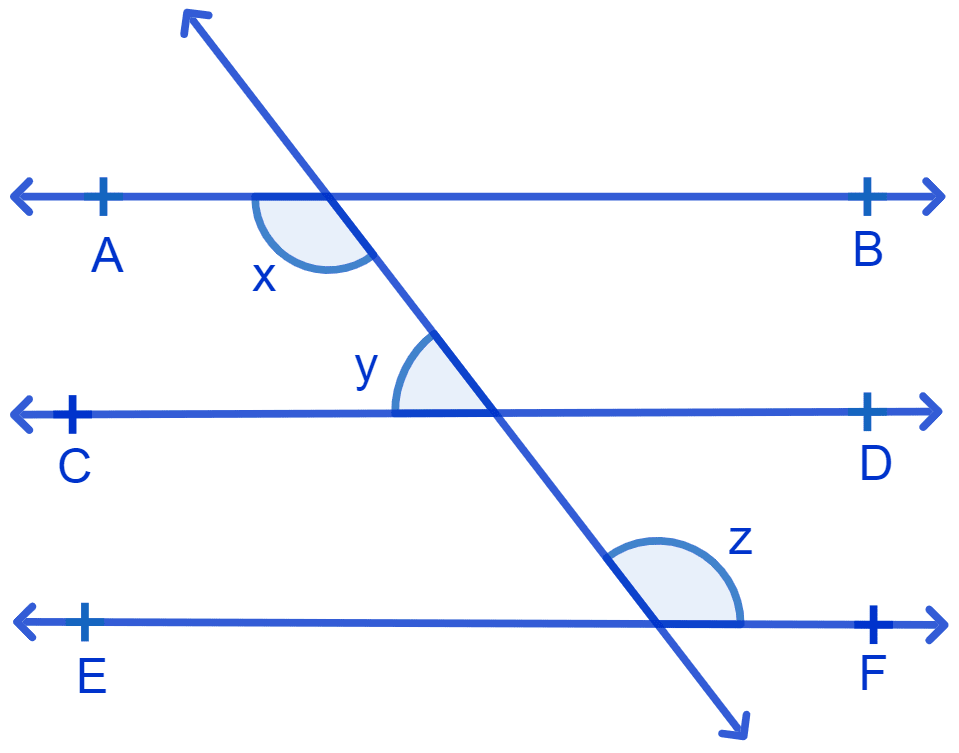
In Fig. if AB || CD, CD || EF and y : z = 3 : 7, find x.