Mathematics
In quadrilateral ABCD, ∠A = 45°, ∠B = 55° and ∠D = 60°; the quadrilateral is:
concave
convex
right angled
none of these
Geometrical Shapes
7 Likes
Answer
As we know, the sum of all the angles in a quadrilateral is 360°.
In quadrilateral ABCD, ∠A = 45°, ∠B = 55° and ∠D = 60°.
∠A + ∠B + ∠C + ∠D = 360°
⇒ 45° + 55° + ∠C + 60° = 360°
⇒ 160° + ∠C = 360°
⇒ ∠C = 360° - 160°
⇒ ∠C = 200°
According to the definition of a concave polygon, if at least one internal angle of a polygon is more than 180°, then the polygon is concave.
Hence, option 1 is the correct option.
Answered By
4 Likes
Related Questions
The value of x + y + z + r is:
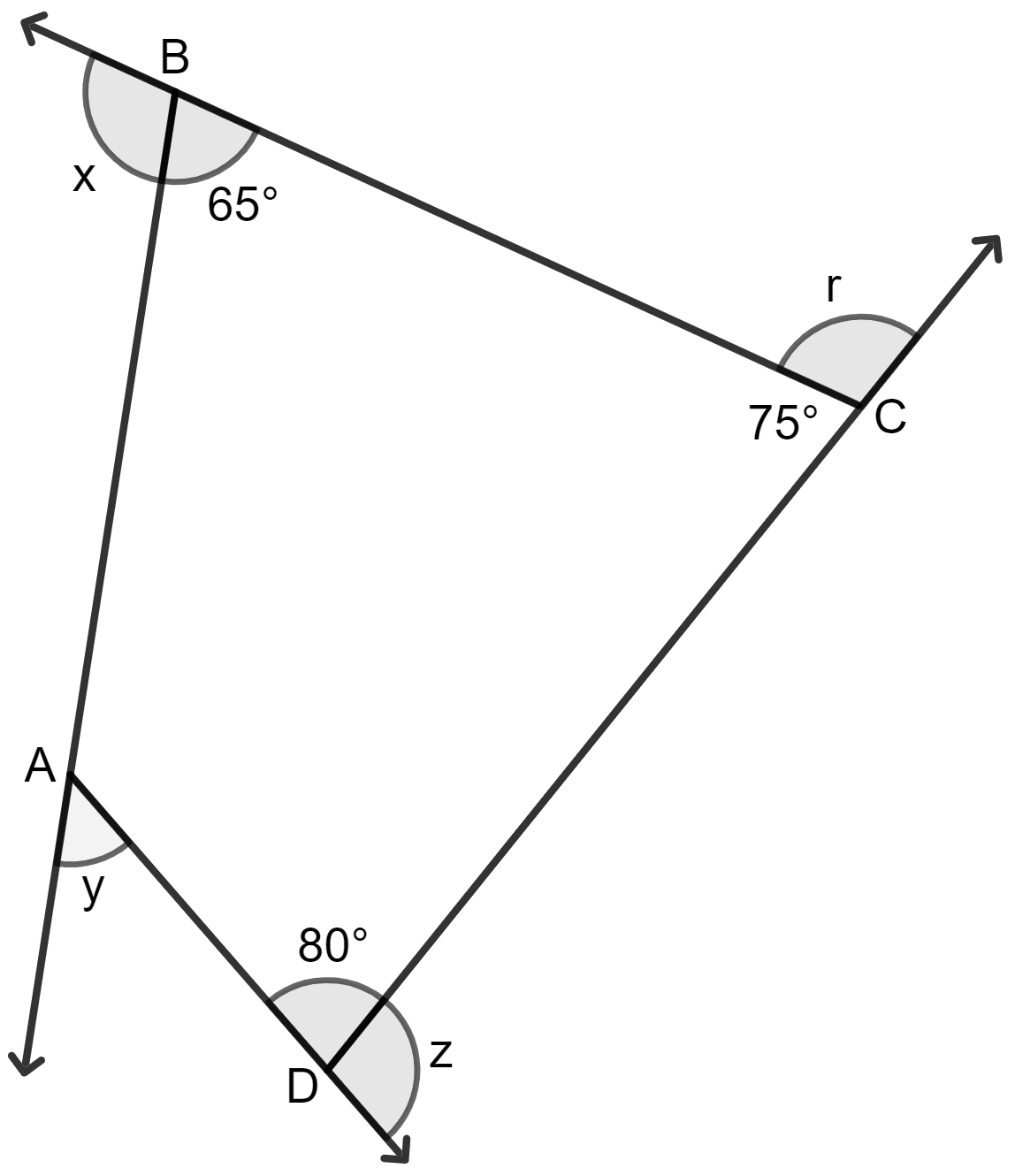
180°
270°
360°
720°
The angles of a quadrilateral are in the ratio in the ratio 2 : 5 : 7 : 4. The largest angle is:
40°
100°
140°
80°
In quadrilateral ABCD, ∠D = 40°, ∠C = 80° AP bisects angle A and BP bisects angle ∠B; then ∠APB is equal:
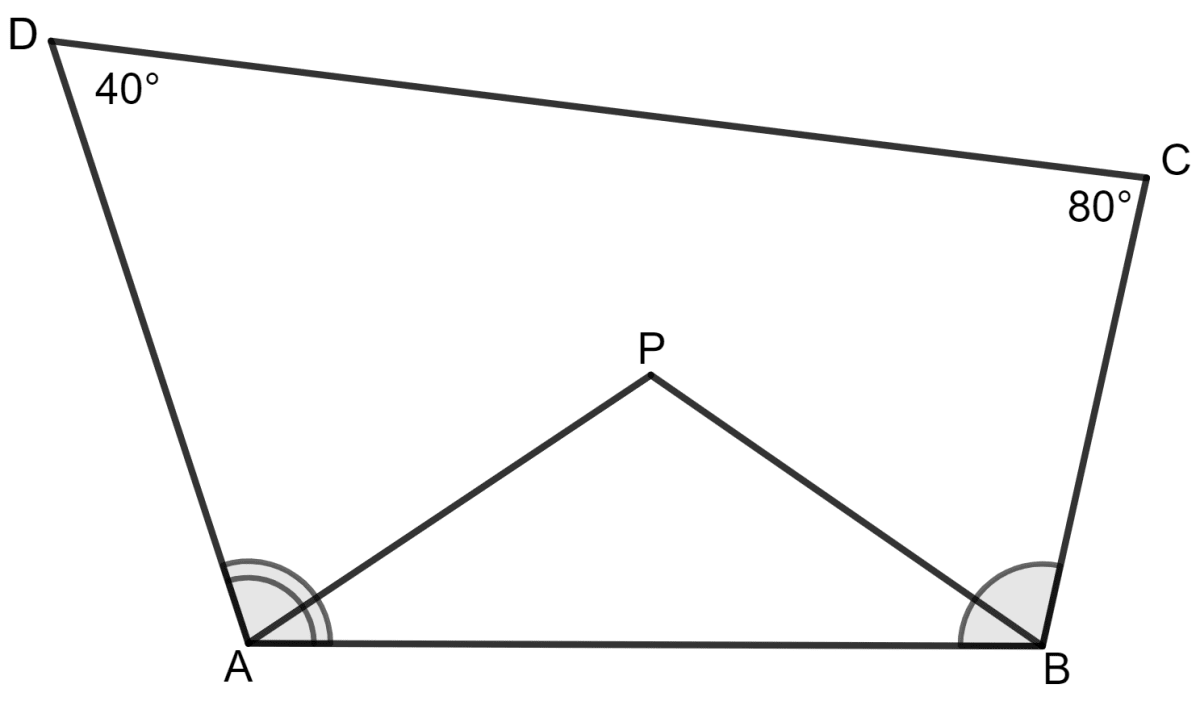
90°
120°
90°
60°
The sum of interior angles of a polygon is 900°. The number of side in this polygon is:
5
7
9
11