Mathematics
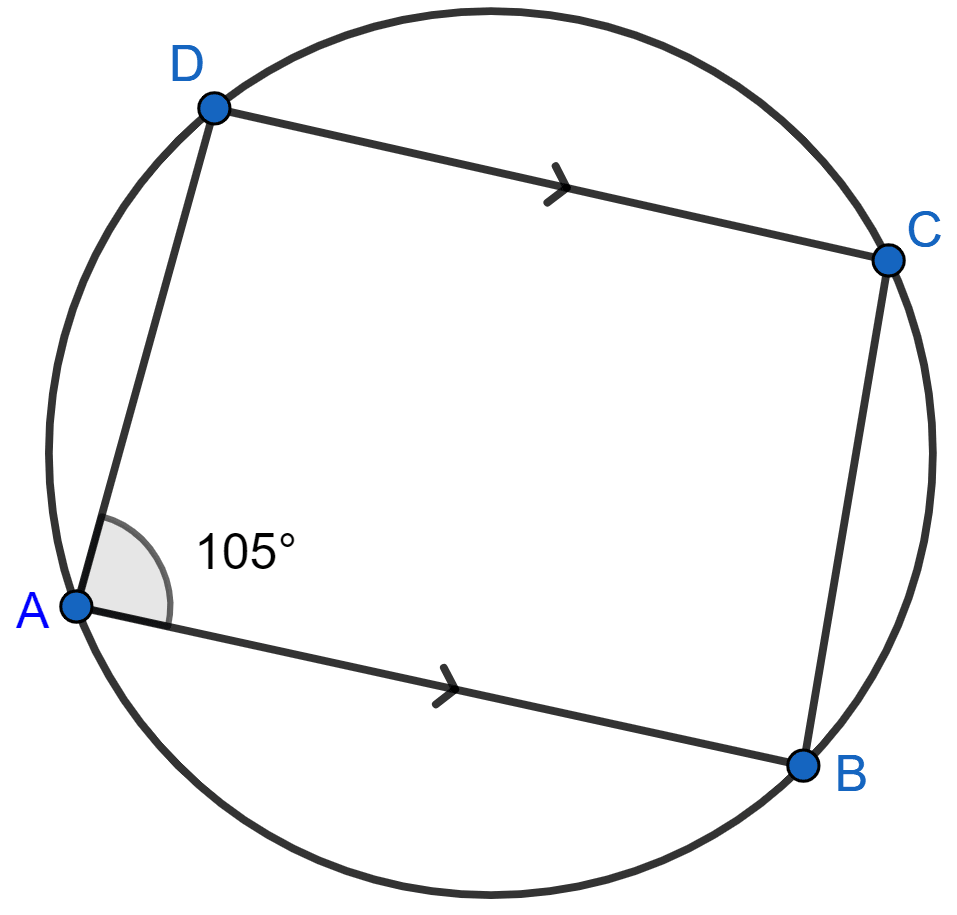
In the figure, given below, find :
(i) ∠BCD,
(ii) ∠ADC,
(iii) ∠ABC.
Show steps of your working.
Circles
11 Likes
Answer
(i) We know that,
Sum of opposite angles in a cyclic quadrilateral is 180°.
⇒ ∠BCD + ∠DAB = 180°
⇒ ∠BCD + 105° = 180°
⇒ ∠BCD = 180° - 105° = 75°.
Hence, ∠BCD = 75°.
(ii) Sum of co-interior angles in a trapezium = 180°.
⇒ ∠ADC + ∠DAB = 180°
⇒ ∠ADC + 105° = 180°
⇒ ∠ADC = 180° - 105° = 75°.
Hence, ∠ADC = 75°.
(iii) We know that, the sum of angles in a quadrilateral is 360°
So,
⇒ ∠ADC + ∠DAB + ∠BCD + ∠ABC = 360°
⇒ 75° + 105° + 75° + ∠ABC = 360°
⇒ ∠ABC = 360° - 255°
⇒ ∠ABC = 105°.
Hence, ∠ABC = 105°.
Answered By
7 Likes
Related Questions
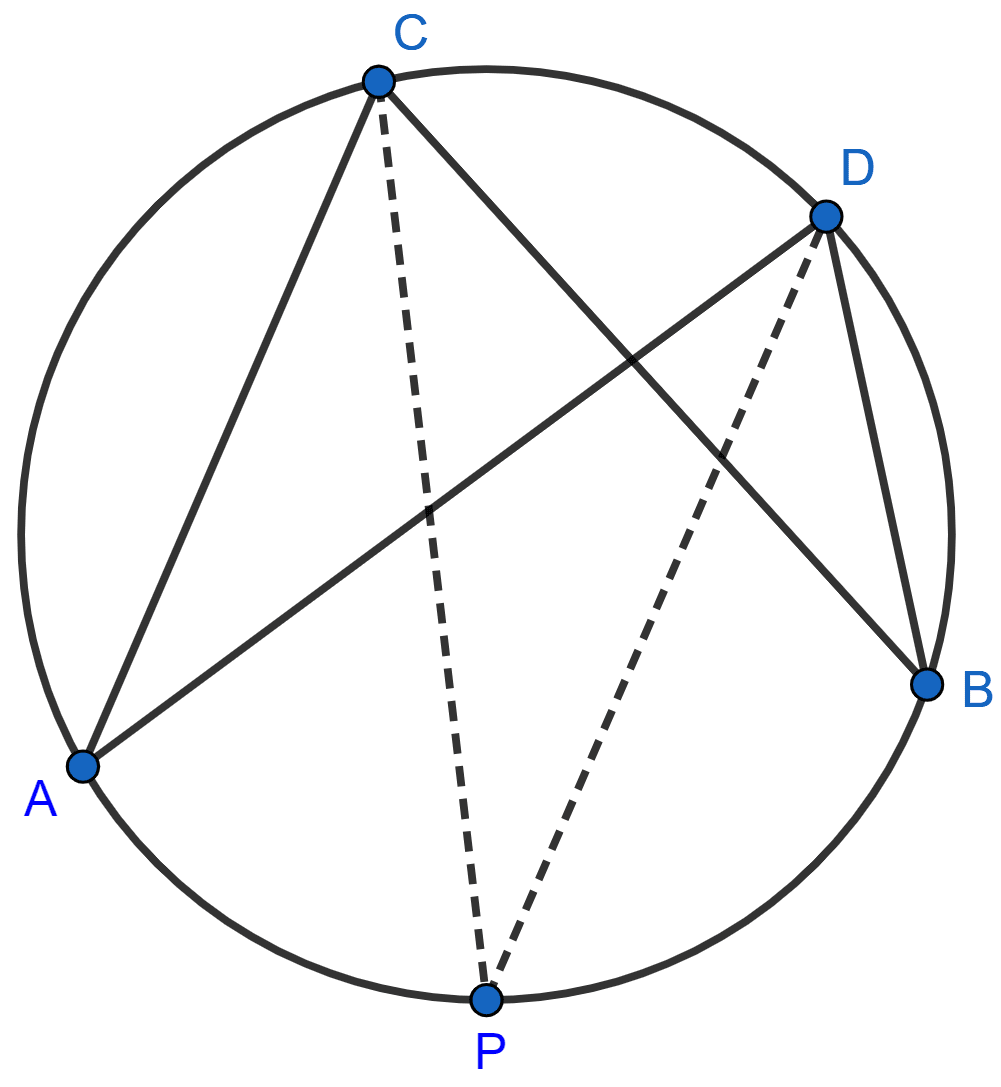
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

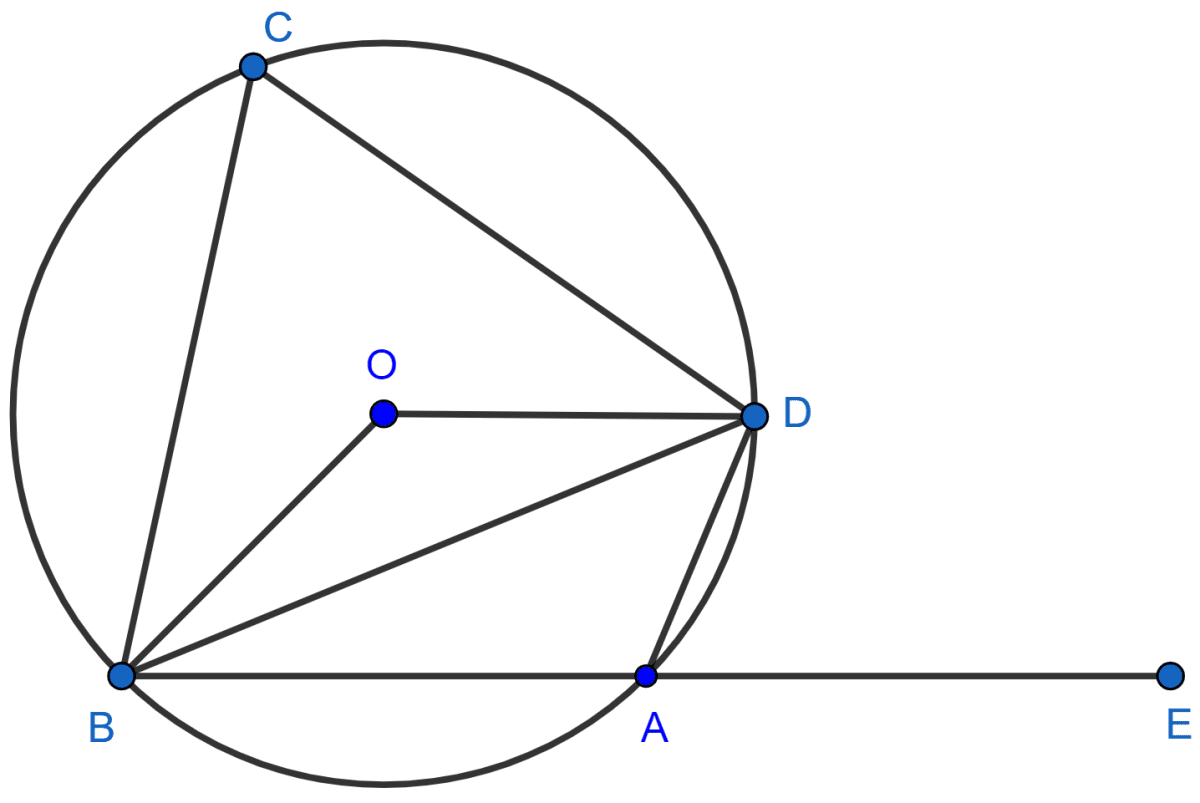
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED

In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD