Mathematics
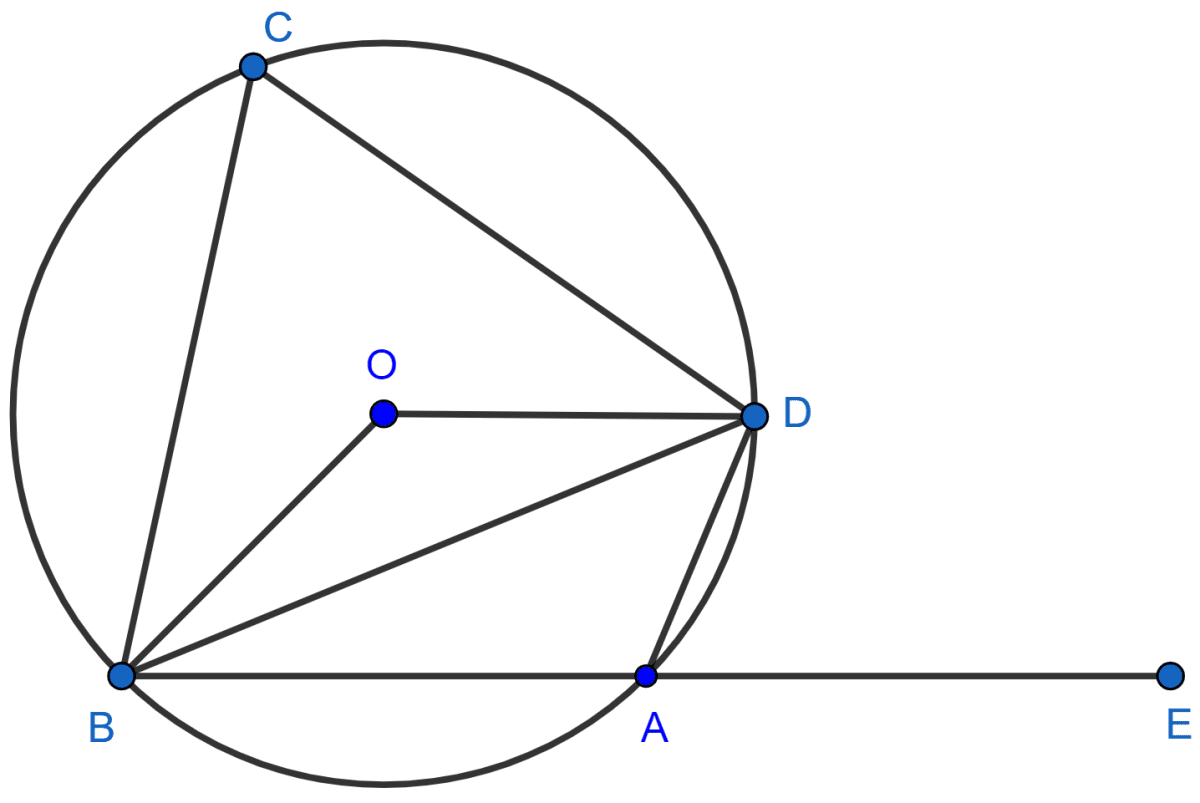
In the given figure, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B.
Prove that : AB = BE.

Circles
1 Like
Answer
Join OB.
From figure,

∠OBA = 90° [As angle in a semi-circle is a right angle]
∴ OB is perpendicular to AE.
We know that,
The perpendicular draw from the centre to a chord bisects the chord.
∴ AB = BE.
Hence, proved that AB = BE.
Answered By
1 Like
Related Questions
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED

In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD