Mathematics
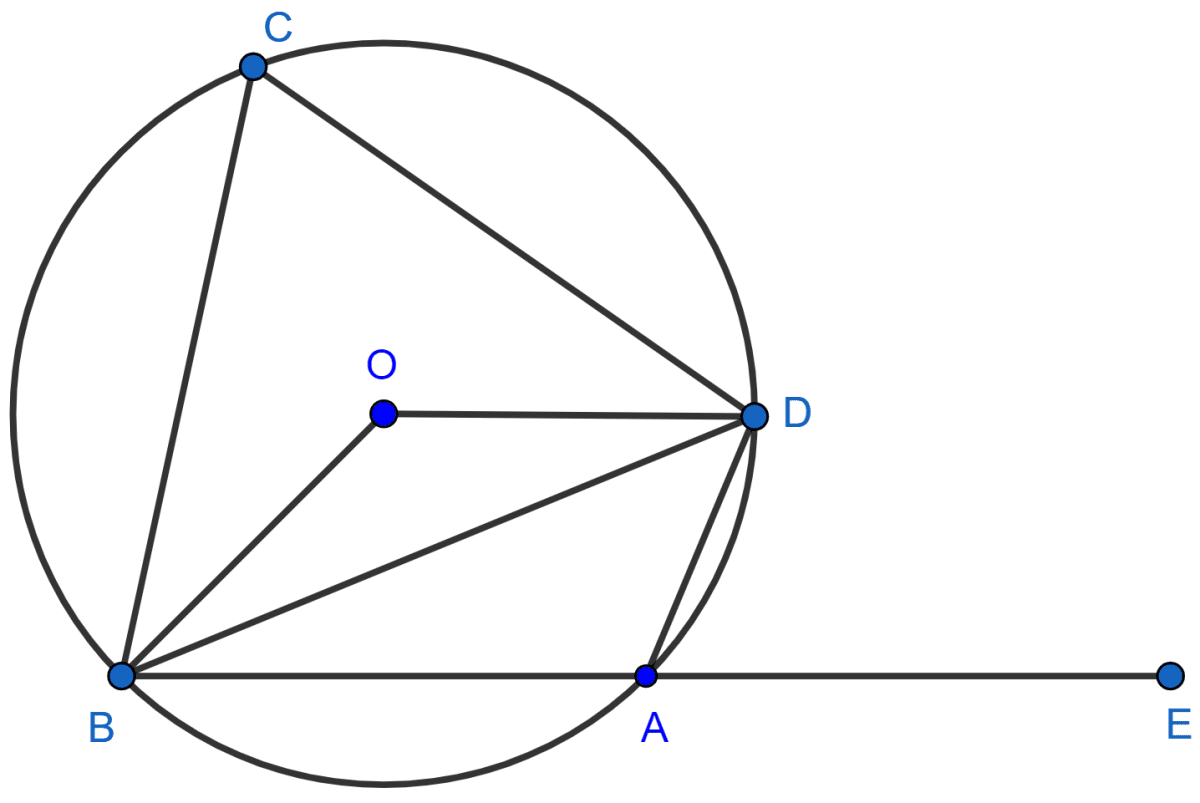
In the given figure, O is the center of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC. Show your steps of working.

Circles
18 Likes
Answer
Join AC.

As, OA = OC = radius of circle.
Let ∠OAC = ∠OCA = x [Angles opposite to equal sides are equal]
We know that,
Sum of angles of triangle = 180°
∴ ∠OAC + ∠OCA + ∠AOC = 180°
⇒ x + x + ∠AOC = 180°
⇒ ∠AOC = 180° - 2x
From figure,
⇒ ∠BAC = ∠BAO + OAC = 30° + x
⇒ ∠BCA = ∠BCO + OCA = 40° + x
Now, in ∆ABC
⇒ ∠ABC = 180° - ∠BAC - ∠BCA [Angle sum property of a triangle]
= 180° - (30° + x) - (40° + x)
= 180° - 30° - x - 40° - x
= 180° - 70° - 2x
= 110° - 2x
We know that,
Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
∴ ∠AOC = 2∠ABC
⇒ 180° - 2x = 2(110° - 2x)
⇒ 180° - 2x = 220° - 4x
⇒ -2x + 4x = 220° - 180°
⇒ 2x = 40°
⇒ x = 20°.
Thus, ∠AOC = 180° - 2x = 180° - 2(20°)
= 180° - 40° = 140°.
Hence, ∠AOC = 140°.
Answered By
11 Likes
Related Questions
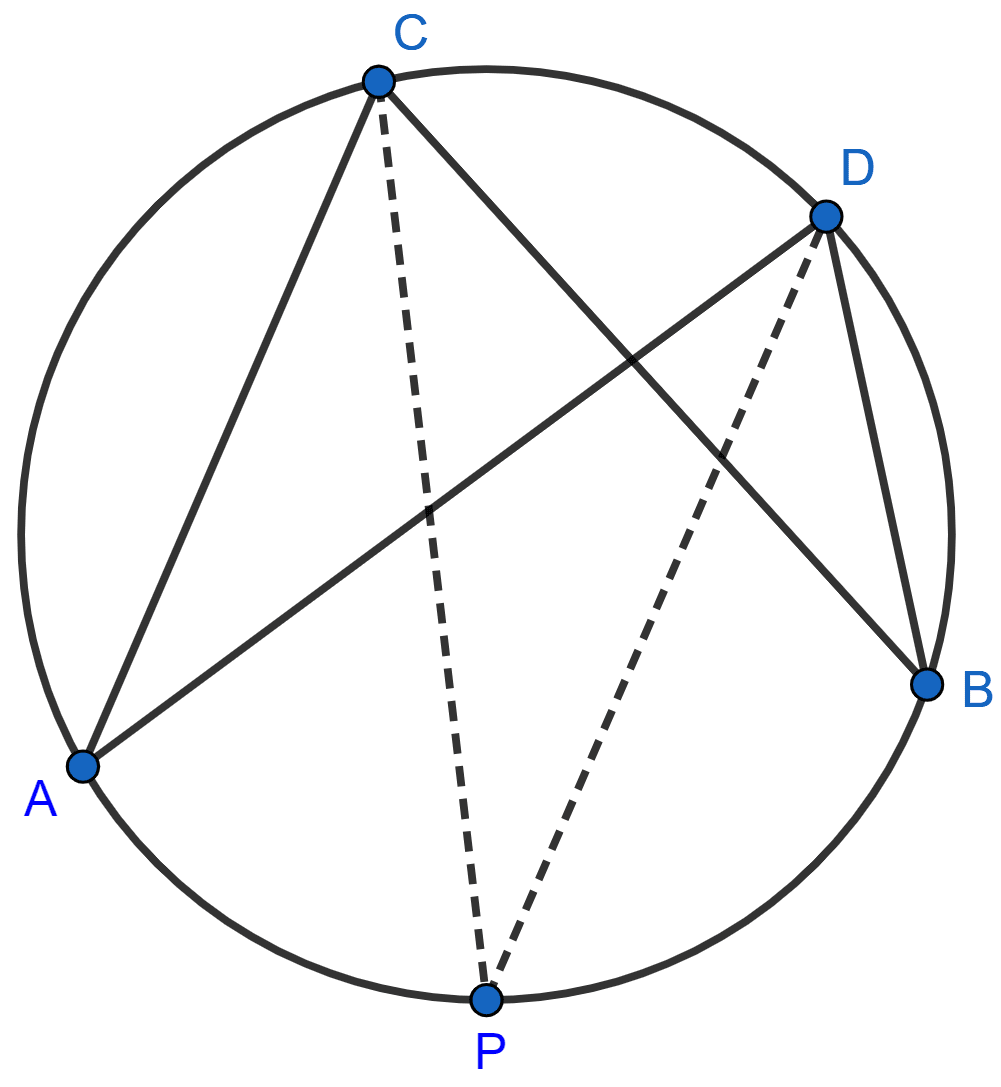
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED

In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD