For the linear equation, given below, draw the graph and then use the graph drawn to find the area of a triangle enclosed by the graph and the co-ordinate axes :

7 - 3 (1 - y) = - 5 + 2x.

7 - 3 (1 - y) = - 5 + 2x

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = 0, then 7 - 3 (1 - y) = - 5 + 2 $\times$ 0 ⇒ y = -3

Let x = 4.5, then 7 - 3 (1 - y) = - 5 + 2 $\times$ 4.5 ⇒ y = 0

Let x = 6, then 7 - 3 (1 - y) = - 5 + 2 $\times$ 6 ⇒ y = 1

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

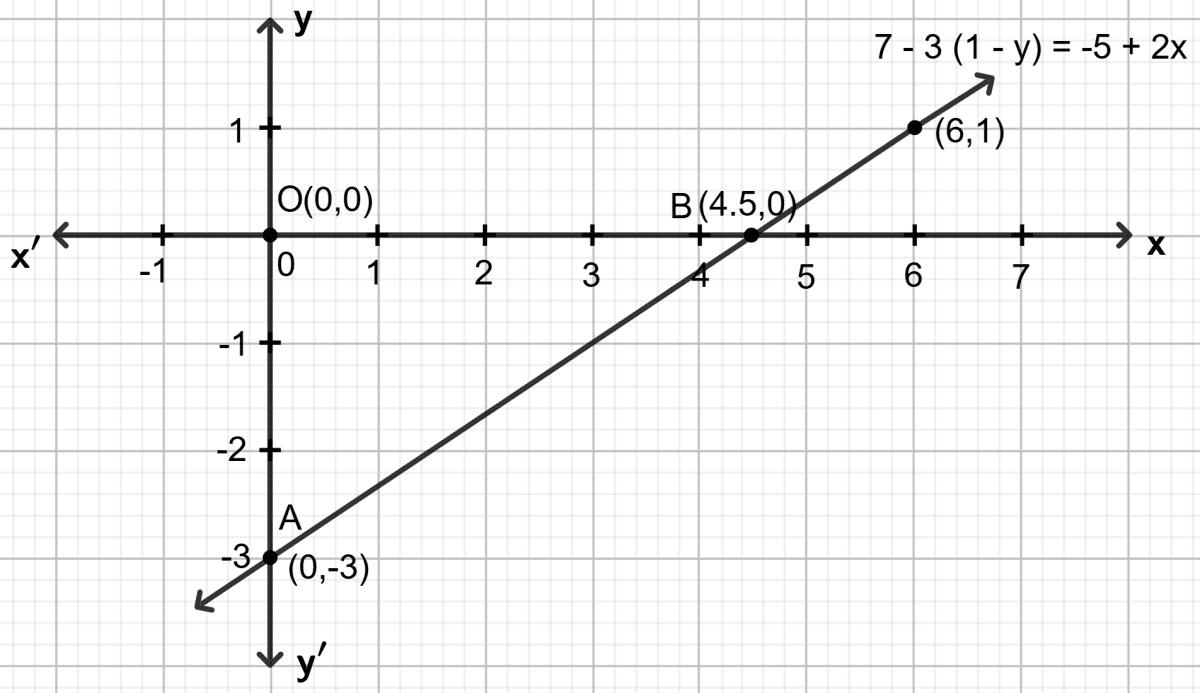
The area of the triangle ABO will be = $\dfrac{1}{2} \times$ base $\times$ altitude

= $\dfrac{1}{2}$ $\times$ OA $\times$ OB

= $\dfrac{1}{2}$ $\times$ 3 $\times$ 4.5

= 6.75 square unit

Hence, the area of triangle = 6.75 square unit.