Mathematics
O is center of the the circle and ∠AOB = 60°. The length of chord AB is :
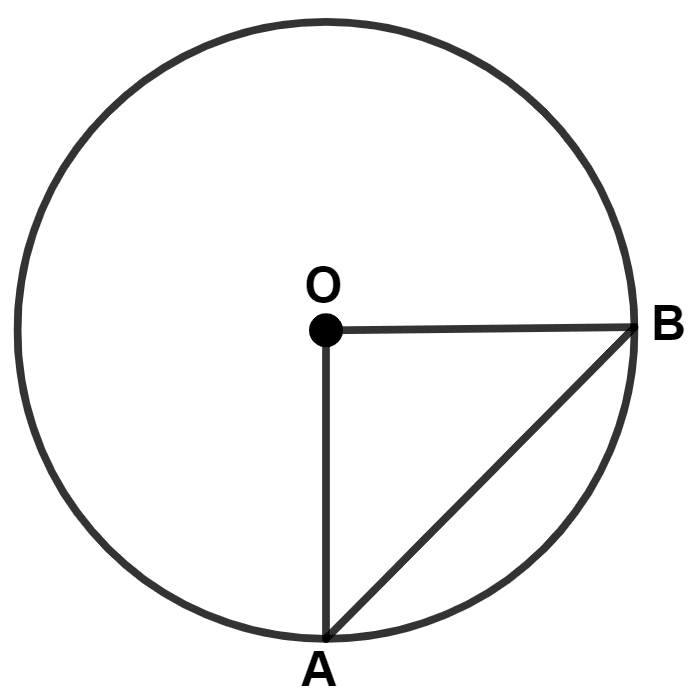
equal to radius of the circle
equal to the side of a regular pentagon
bigger than the radius of the circle
smaller than the radius of the circle.
Constructions
3 Likes
Answer
From figure,
⇒ OA = OB (Radius of same circle)
⇒ ∠OBA = ∠OAB = x (let) [In a triangle angles opposite to equal sides are equal.]
In △ AOB,
By angle sum property of triangle,
⇒ ∠OBA + ∠OAB + ∠AOB = 180°
⇒ x + x + 60° = 180°
⇒ 2x + 60° = 180°
⇒ 2x = 180° - 60°
⇒ 2x = 120°
⇒ x = = 60°
⇒ ∠OBA = ∠OAB = ∠AOB = 60°.
∴ AOB is an equilateral triangle.
∴ AB = OA = OB
∴ AB = Radius of circle.
Hence, Option 1 is the correct option.
Answered By
2 Likes
Related Questions
Using a ruler and a compass, construct a triangle ABC in which AB = 7 cm, ∠CAB = 60° and AC = 5 cm. Construct the locus of :
(i) points equidistant from AB and AC.
(ii) points equidistant from BA and BC.
Hence construct a circle touching the three sides of the triangle internally.
Construct a triangle ABC in which AB = 5 cm, BC = 6.8 cm and median AD = 4.4 cm. Draw incircle of this triangle.
Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
In triangle ABC, ∠ABC = 90°, side AB = 6 cm, side BC = 7.2 cm and BD is perpendicular to side AC. Draw circumcircle of triangle BDC and then state the length of the radius of this circumcircle drawn.