Mathematics
OABC is a rhombus whose three vertices A, B and C lie on a circle with centre O.
(i) If the radius of the circle is 10 cm, find the area of the rhombus.
(ii) If the area of the rhombus is cm2, find the radius of the circle.
Circles
2 Likes
Answer
(i) Given, radius = 10 cm
In rhombus OABC,
OC = 10 cm
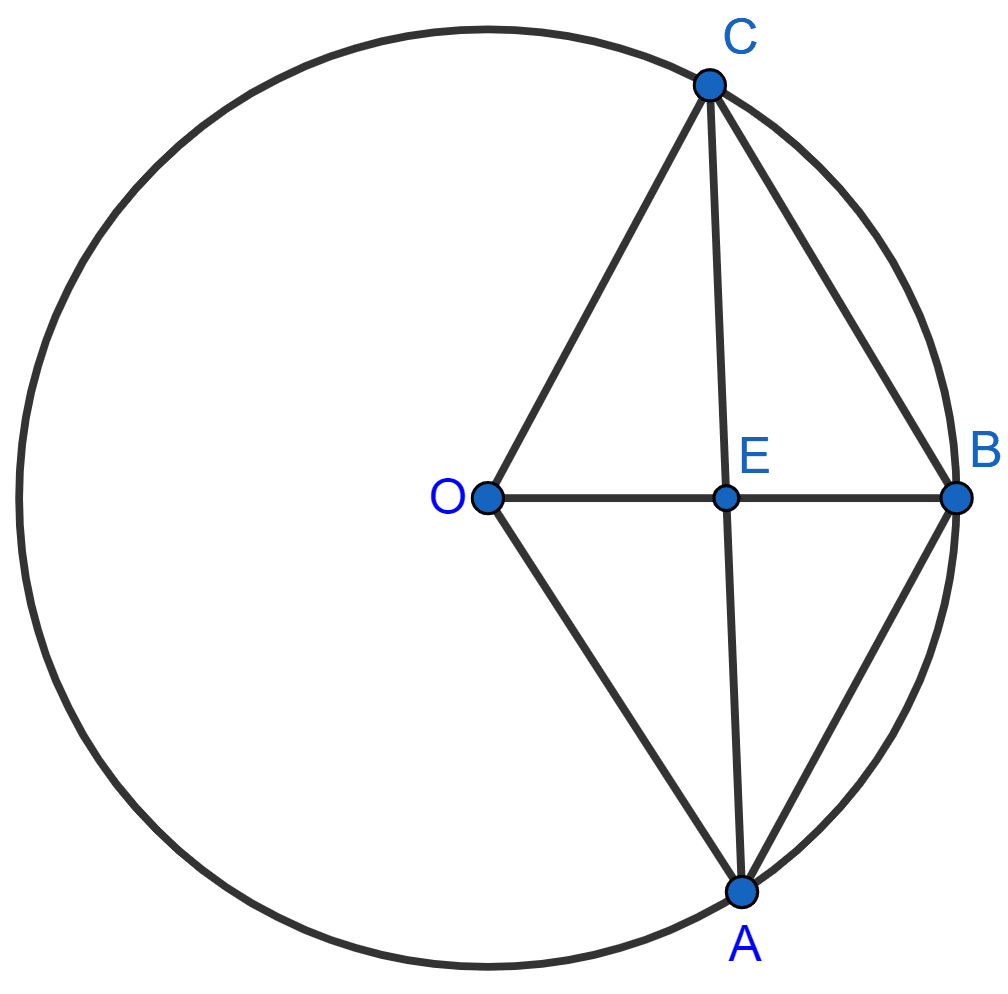
As, diagonal of rhombus bisect each other.
OE = x OB = x 10 = 5 cm.
Now, in right ∆OCE,
⇒ OC2 = OE2 + EC2
⇒ 102 = 52 + EC2
⇒ EC2 = 100 - 25 = 75
⇒ EC = .
Hence, AC = 2 x EC = 2 x cm.
We know that,
Area of rhombus =
=
=
= = 86.60 cm2.
Hence, area of rhombus = 86.60 cm2.
(ii) Given, area of rhombus = cm2
We know that,
Diagonal of rhombus divides it into two equilateral triangles.
∴ Area of rhombus OABC = 2 x area of ∆OAB
⇒ Area of rhombus OABC = 2 x
Hence, radius of circle = 8 cm.
Answered By
1 Like
Related Questions
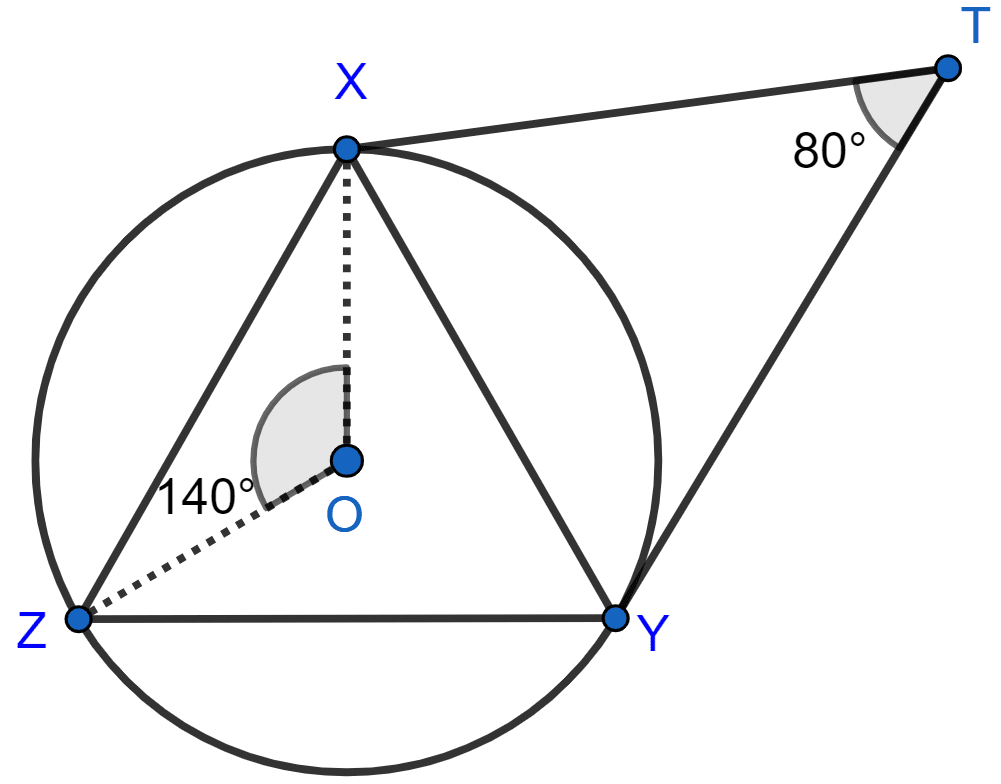
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

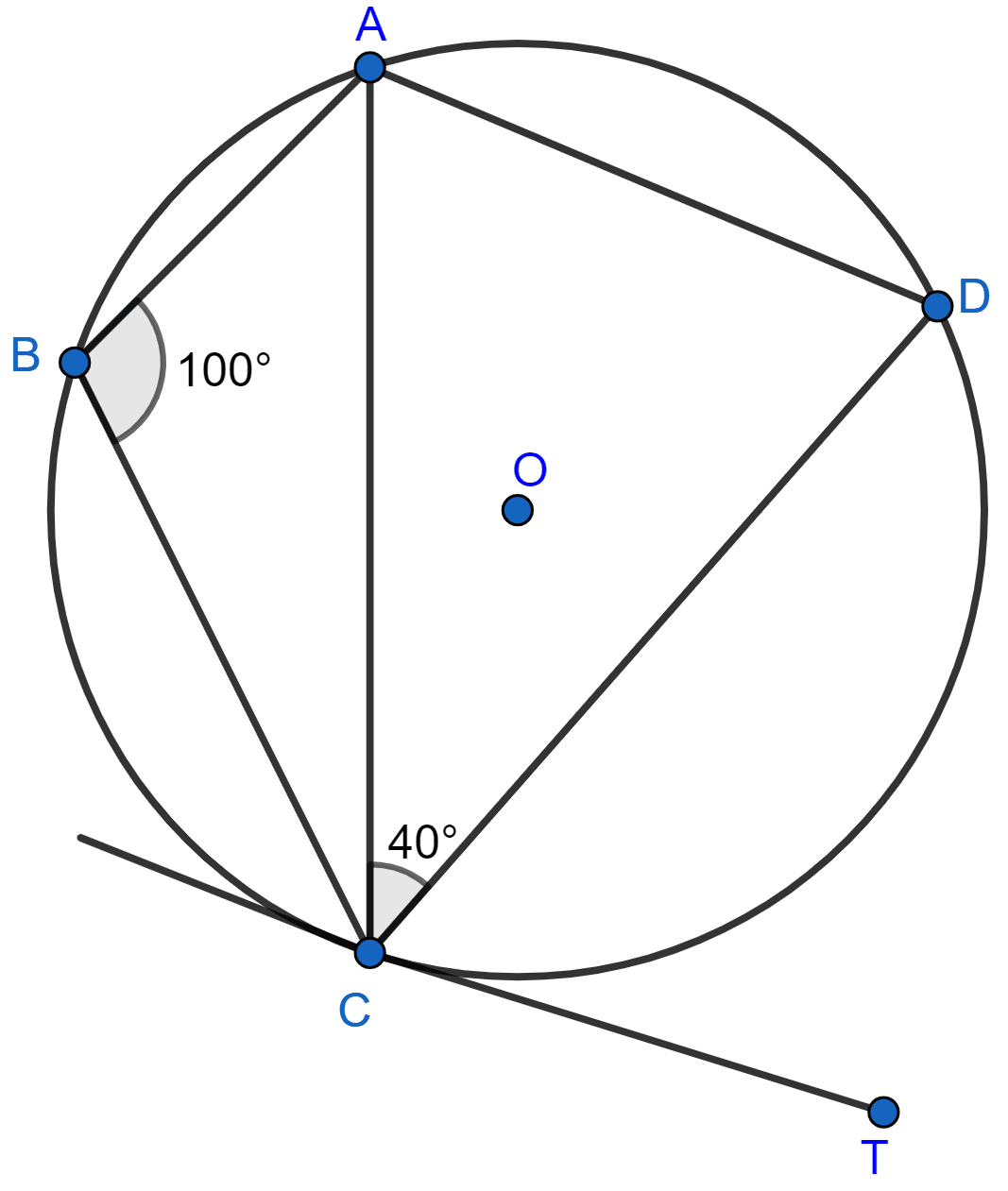
In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
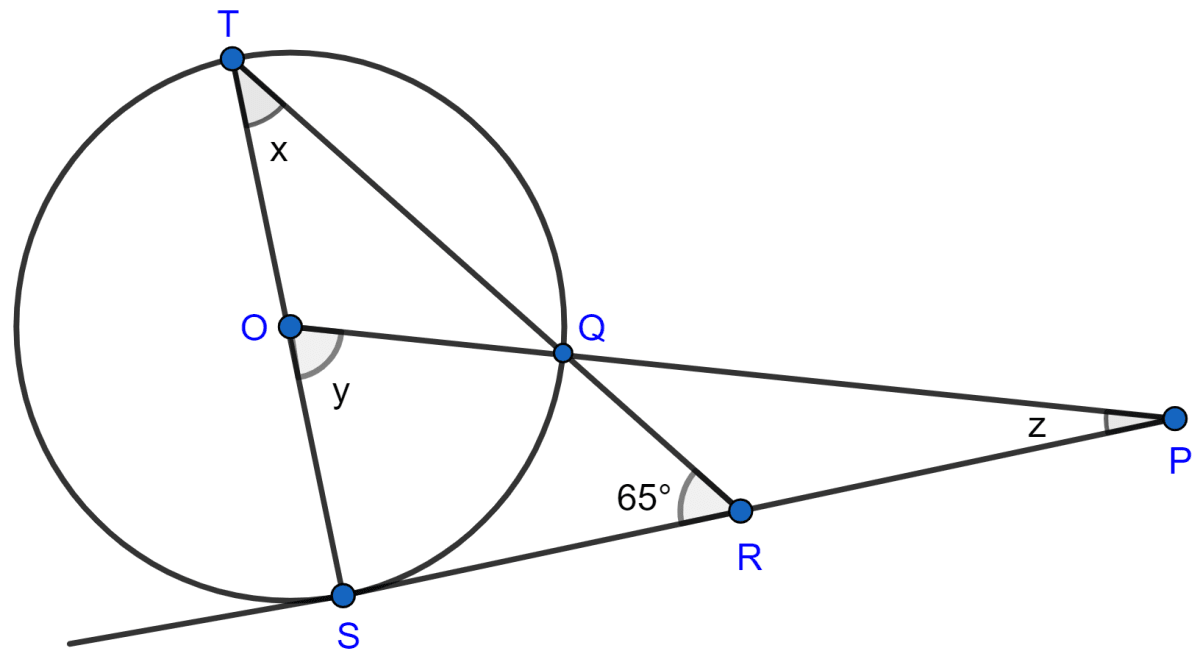
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.