Mathematics
P, Q and R are the mid-points of the sides of an equilateral triangle XYZ. Then PQR is
Mid-point Theorem
2 Likes
Answer
an equilateral triangle
Reason
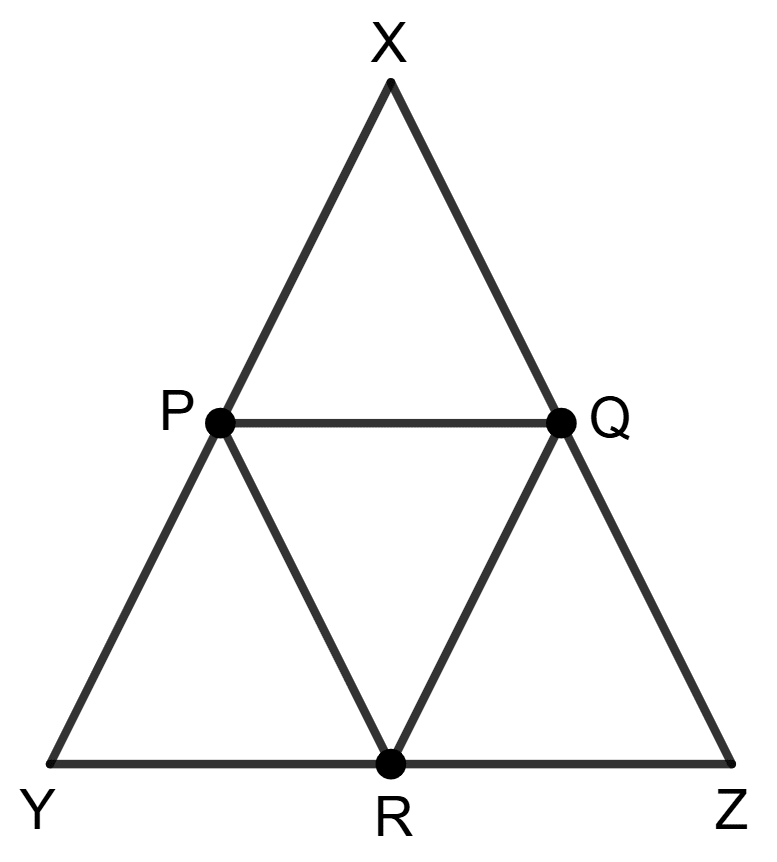
Given,
XYZ is an equilateral triangle.
⇒ XY = YZ = ZX
P, Q and R are the mid-points of the sides of an equilateral triangle XYZ.
By mid-point theorem,
The line joining mid-point of any two sides of a triangle is parallel and is equal to half of third side.
Since, P and Q are mid-points of sides XY and XZ,
∴ PQ || YZ and PQ = YZ
(As we know, XY = YZ = ZX)
⇒ PQ = XZ ……………….(1)
And, Q and R are mid-points of sides XZ and YZ,
∴ QR || XY and QR = XY
(As we know, XY = YZ = ZX)
⇒ QR = ……………….(2)
Similarly, P and R are mid-points of sides XY and YZ,
∴ PR || XZ and PR = XZ
(As we know, XY = YZ = ZX)
⇒ PR = YZ ……………….(3)
From equation (1), (2) and (3), we can clearly say that
⇒ PQ = QR = PR = YZ
⇒ PQ = QR = PR
Hence, PQR is also an equilateral triangle.
Answered By
2 Likes
Related Questions
In trapezium ABCD, AB // DC. M is mid-point of AD and N is mid-point of BC.
(i) If AB = 8 cm and DC = 11 cm, find MN.
(ii) If AB = 5.7 cm and MN = 6.2 cm, find DC.
Assertion (A): Using the information in the given figure, we have PQ = 10 cm.
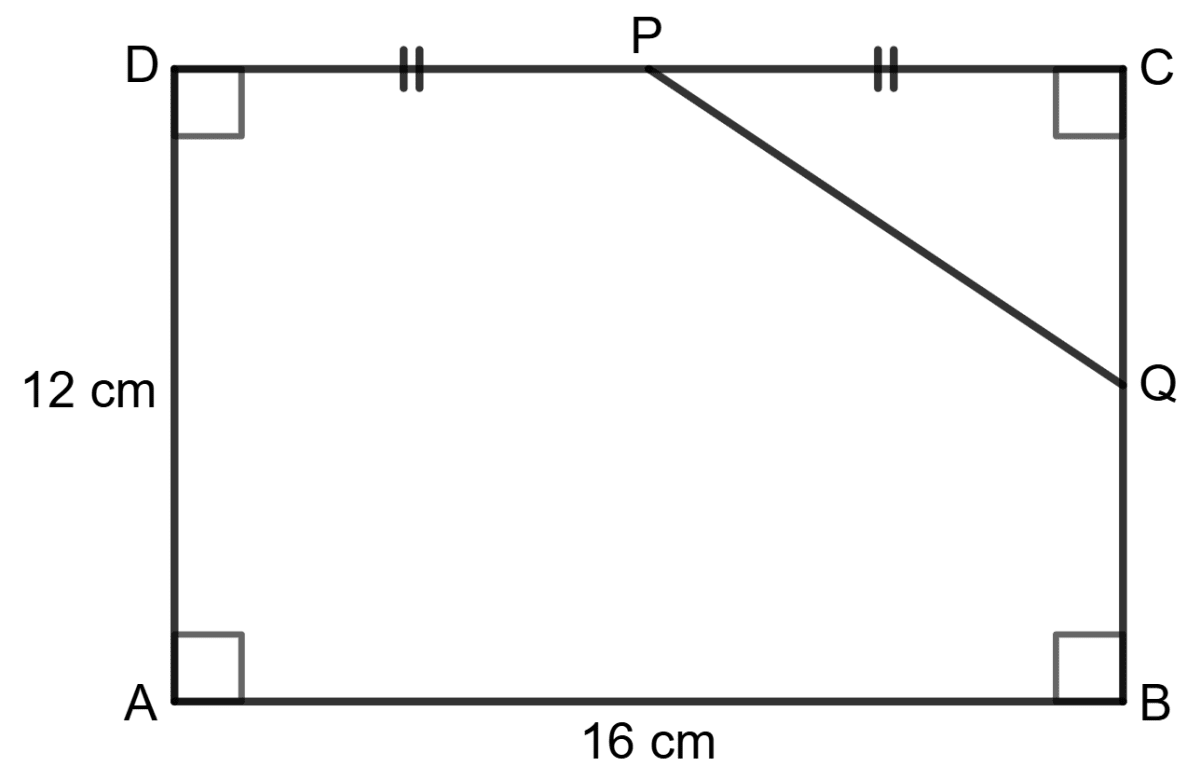
Reason (R): In right-triangle DAB, DB = 20 cm.

- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.