Mathematics
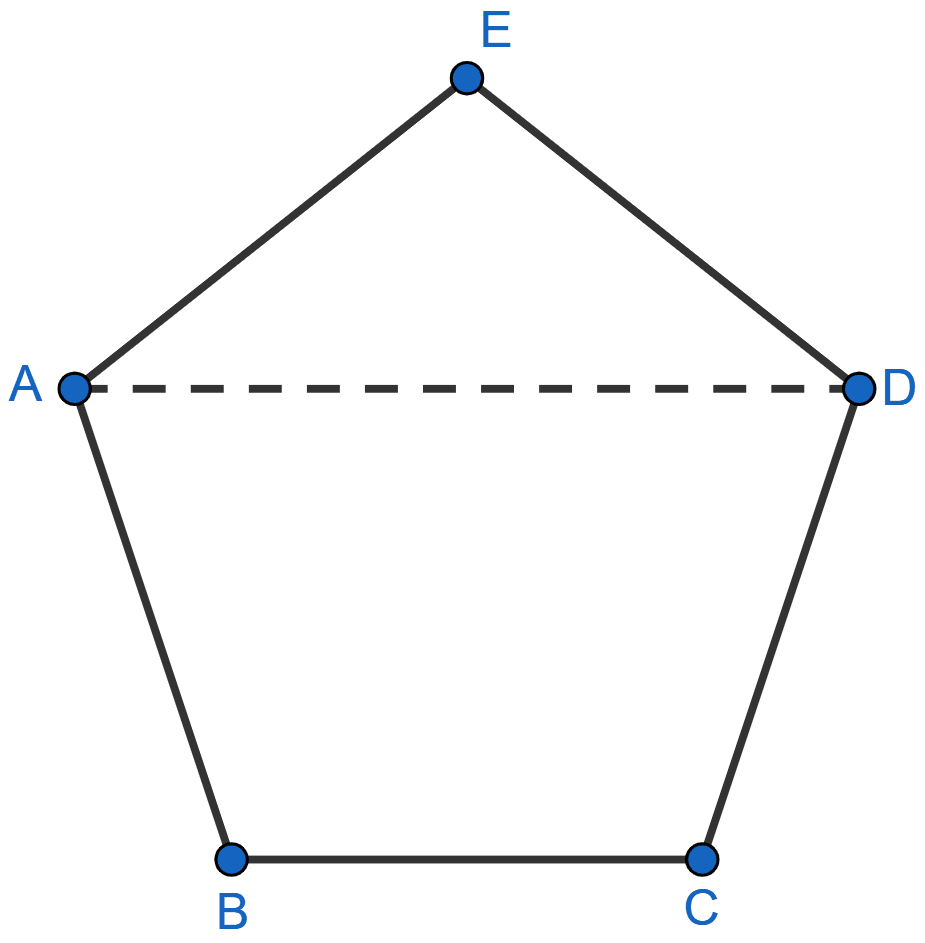
Prove that any four vertices of a regular pentagon are concyclic (lie on the same circle).
Circles
1 Like
Answer
Let ABCDE be a regular pentagon.
∴ ∠ABC = ∠BCD = ∠CDE = ∠DEA = ∠EAB.
Interior angle of a regular polygon is given by :
So, each interior angle of a regular pentagon = = 108°.
In △AED,
AE = ED [Sides of a regular pentagon are equal]
∴ ∠EAD = ∠EDA [Angles opposite to equal sides are equal] ………(1)
⇒ ∠AED + ∠EAD + ∠EDA = 180°
⇒ 108° + ∠EAD + ∠EAD = 180°
⇒ 2∠EAD = 180° - 108°
⇒ 2∠EAD = 72°
⇒ ∠EAD =
⇒ ∠EAD = 36°.
∴ ∠EDA = 36°.
From figure,
∠BAD = ∠BAE - ∠EAD = 108° - 36° = 72°.
In quadrilateral ABCD,
∠BAD + ∠BCD = 72° + 108° = 180°.
Since, sum of opposite angles = 180°,
which is possible when the quadrilateral is cyclic quadrilateral.
Hence, proved that ABCD is a cyclic quadrilateral.
Answered By
1 Like
Related Questions
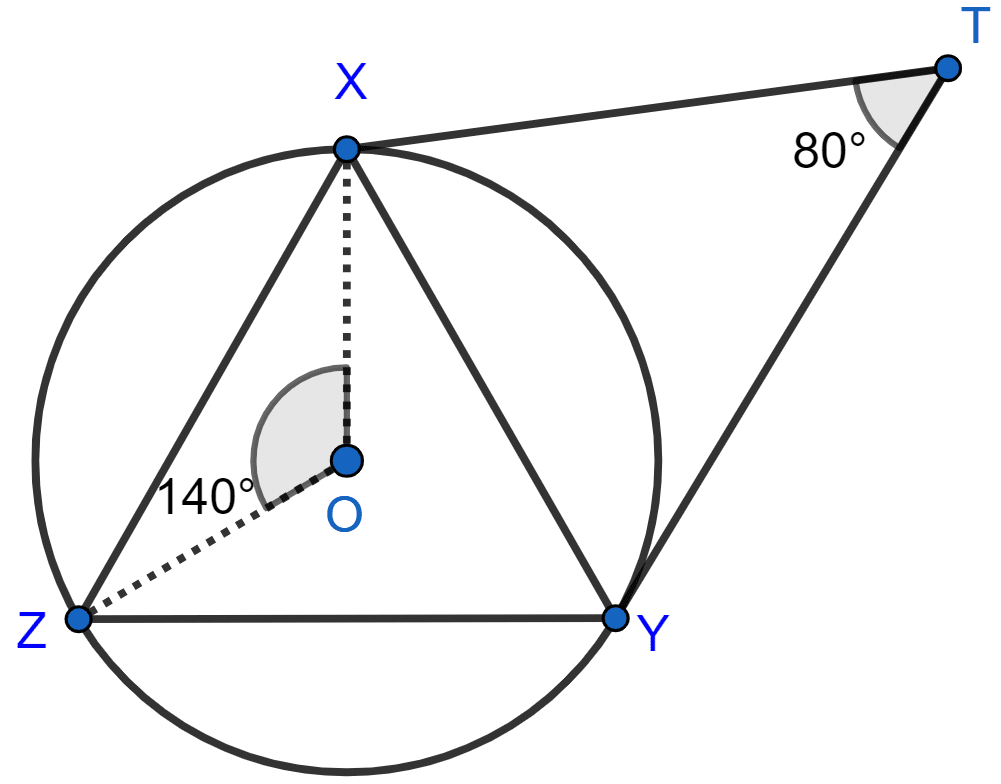
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

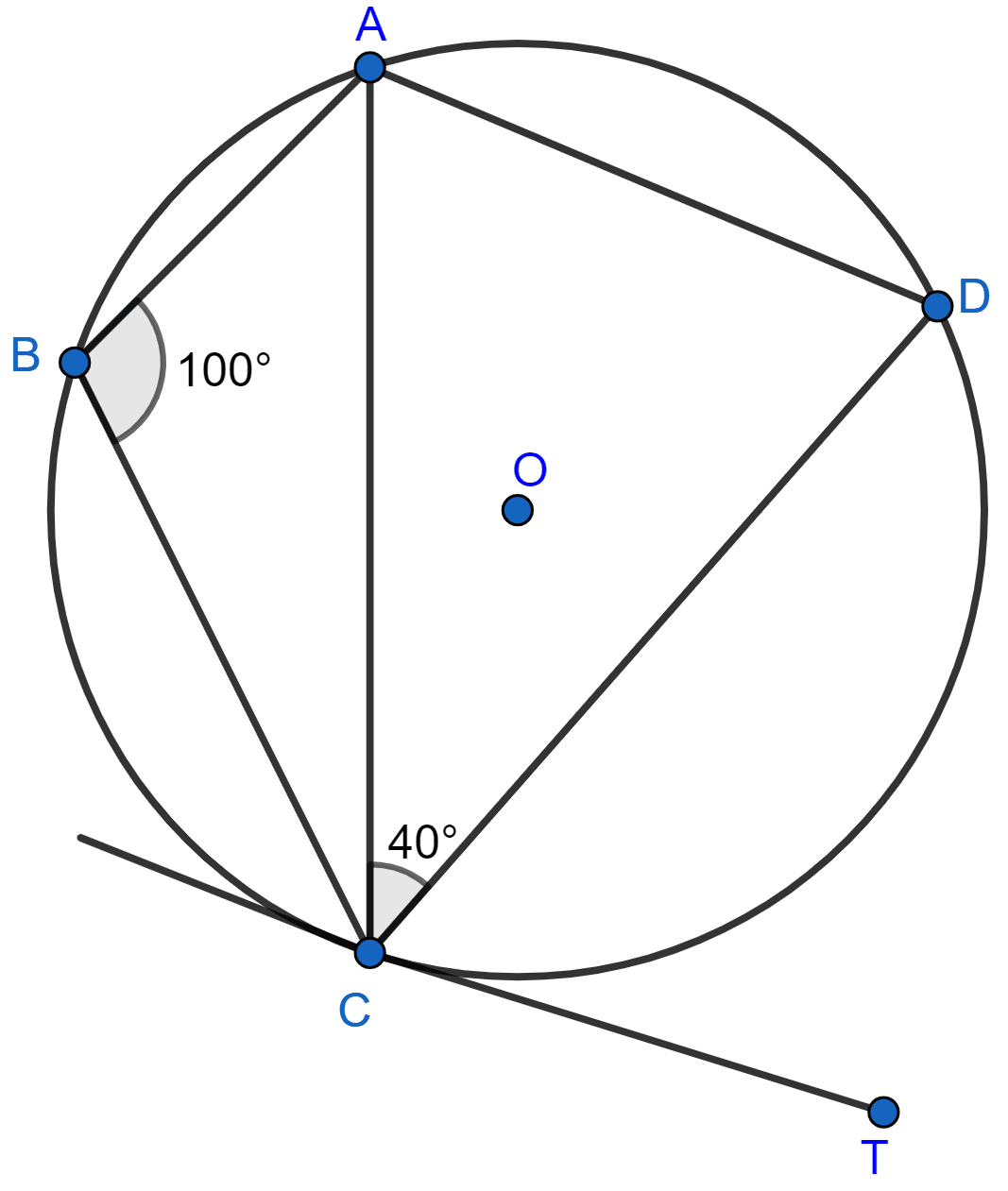
In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
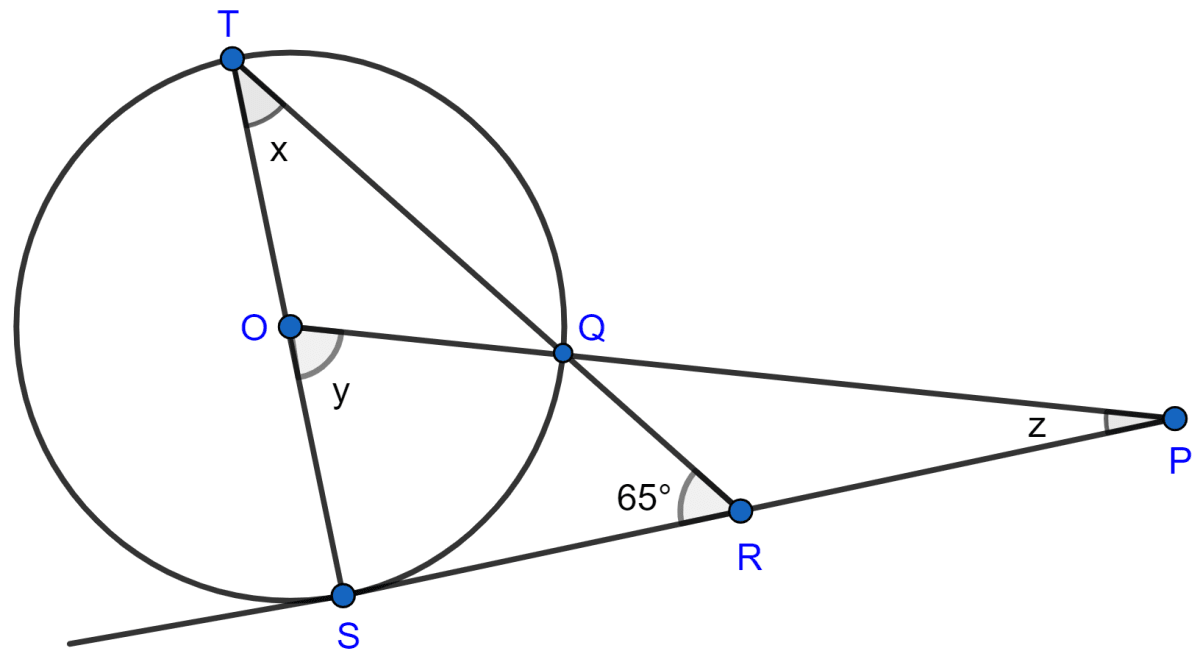
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.