Represent each of the following on different number lines :

$2\sqrt{3}, 2\sqrt{2}, 3 + \sqrt{2}, 3 - \sqrt{2} \text{ and } 2\sqrt{5}$ .

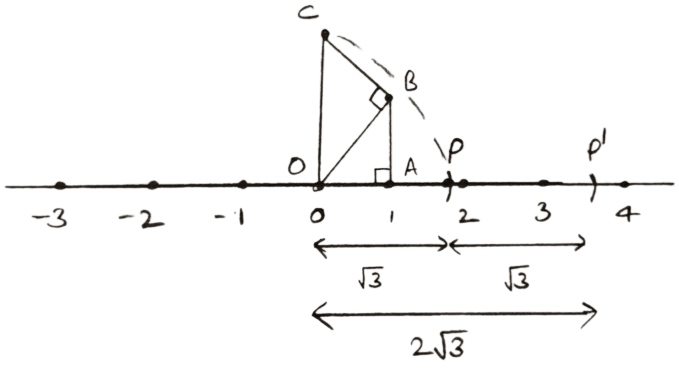
Steps of construction of $2\sqrt{3}$ :

1. Take OA = AB = 1 unit and ∠OAB = 90°, so by pythagoras theorem :
   ⇒ OB² = OA² + AB²
   ⇒ OB² = 1² + 1²
   ⇒ OB² = 1 + 1
   ⇒ OB² = 2
   ⇒ OB = $\sqrt{2}$ unit
2. Draw BC = AB = OA = 1 unit and ∠OBC = 90°.
3. By pythagoras theorem :
   ⇒ OC² = OB² + BC²
   ⇒ OC² = $(\sqrt{2})^2 + 1^2$
   ⇒ OC² = 2 + 1
   ⇒ OC² = 3
   ⇒ OC = $\sqrt{3}$ unit.
4. With point O as center and OC as radius darw an arc which meets the number line at point P.
   OP = OC = $\sqrt{3}$.
5. With P as center and OP as radius draw an arc cutting number line at P', so PP' = $\sqrt{3}$
   OP' = OP + PP' = $\sqrt{3} + \sqrt{3} = 2\sqrt{3}$.

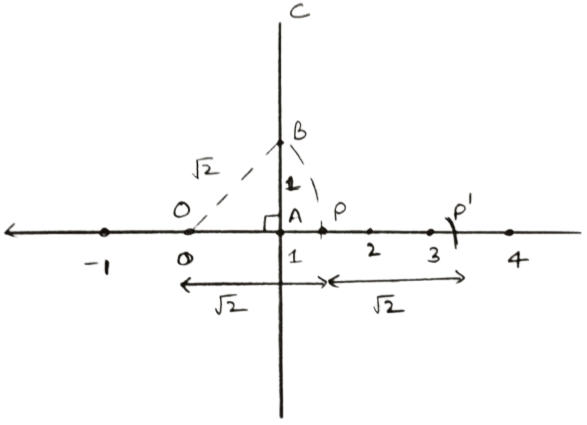
Steps of construction of $2\sqrt{2}$ :

1. Mark O of the number line at point 0.
2. On the same number line, mark 1 as point A i.e., take OA = 1 unit
3. At point A, draw AC perpendicular to the number line.
4. From AC, cut AB = 1 unit = OA, then join A and B.
   Using pythagoras theorem, we get :
   OB² = OA² + AB²
   OB² = 1² + 1²
   OB² = 1 + 1 = 2
   OB = $\sqrt{2}$.
5. Taking point O as center and OB = $\sqrt{2}$ as radius, draw an arc which cuts the number line at point P.
   Clearly, OP = OB = $\sqrt{2}$
6. With P as center and OP as radius draw an arc intersecting number line at P'.
   OP' = OP + PP' = $\sqrt{2} + \sqrt{2} = 2\sqrt{2}$.

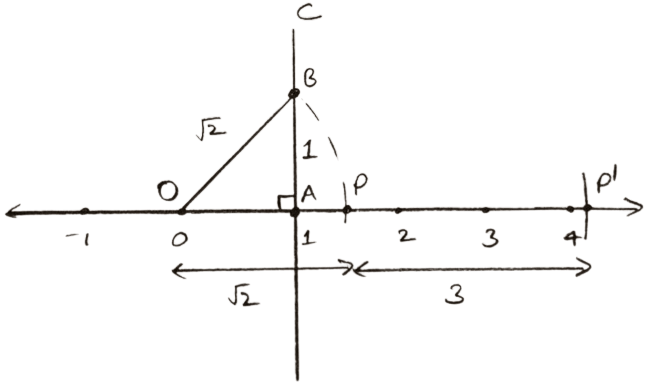
Steps of construction of $3 + \sqrt{2}$

1. Mark O of the number line at point 0.
2. On the same number line, mark 1 as point A i.e., take OA = 1 unit
3. At point A, draw AC perpendicular to the number line.
4. From AC, cut AB = 1 unit = OA, then join O and B.
   Using pythagoras theorem, we get :
   OB² = OA² + AB²
   OB² = 1² + 1²
   OB² = 1 + 1 = 2
   OB = $\sqrt{2}$.
5. Taking point O as center and OB = $\sqrt{2}$ as radius, draw an arc which cuts the number line at point P.
   Clearly, OP = OB = $\sqrt{2}$
6. From point P as center and radius = 3 cm draw an arc intersecting number line at P'.
   OP' = OP + PP' = $\sqrt{2} + 3$.

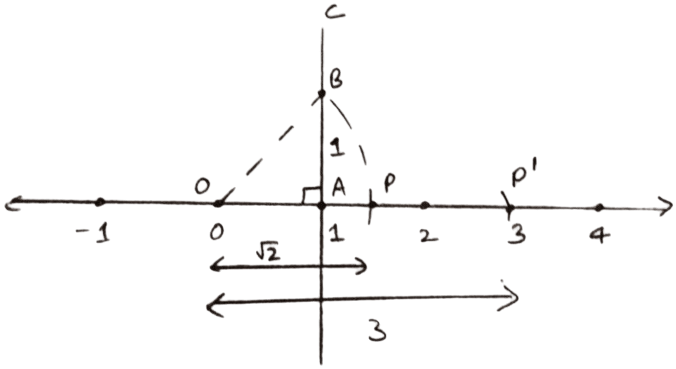
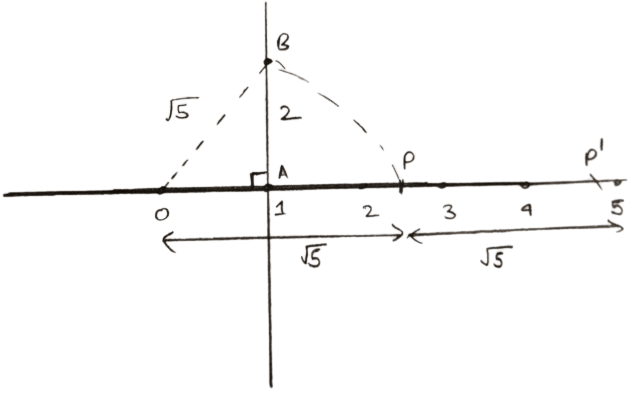
Steps of construction of $3 - \sqrt{2}$

1. Mark O of the number line at point 0.
2. On the same number line, mark 1 as point A i.e., take OA = 1 unit
3. At point A, draw AC perpendicular to the number line.
4. From AC, cut AB = 1 unit = OA, then join O and B.
   Using pythagoras theorem, we get :
   OB² = OA² + AB²
   OB² = 1² + 1²
   OB² = 1 + 1 = 2
   OB = $\sqrt{2}$.
5. Taking point O as center and OB = $\sqrt{2}$ as radius, draw an arc which cuts the number line at point P.
   Clearly, OP = OB = $\sqrt{2}$
6. From point O as center and radius = 3 unit draw an arc intersecting number line at P'.
   PP' = OP' - OP = $3 - \sqrt{2}$.

Steps of construction of $2\sqrt{5}$ :

1. Mark O of the number line at point 0.
2. On the same number line, mark 1 as point A i.e., take OA = 1 unit
3. At point A, draw AC perpendicular to the number line.
4. From AC, cut AB = 2 unit, then join O and B.
   Using pythagoras theorem, we get :
   OB² = OA² + AB²
   OB² = 1² + 2²
   OB² = 1 + 4 = 5
   OB = $\sqrt{5}$.
5. Taking point O as center and OB = $\sqrt{5}$ as radius, draw an arc which cuts the number line at point P.
   Clearly, OP = OB = $\sqrt{5}$
6. From point P as center and OP as radius draw an arc intersecting number line at P'.
   OP' = OP + PP' = $\sqrt{5} + \sqrt{5} = 2\sqrt{5}$.