Mathematics
Restate the following statements with appropriate conditions, so that they become true statements.
(i) All prime numbers are odd.
(ii) Two times a real number is always even.
(iii) For any x, 3x + 1 > 4.
(iv) For any x, x3 ≥ 0.
(v) In every triangle, a median is also an angle bisector.
Mathematics Proofs
2 Likes
Answer
(i) We know that,
A natural number that has exactly two factors, i.e., 1 and the number itself, is a prime number. Example - 2, 3, 5, 7,…….
Hence, all prime numbers greater than 2 are odd.
(ii) Let real number be 1.5
On multiplying by 2, we get :
1.5 × 2 = 3, which is an odd number.
∴ The statement, two times a real number is always even, is incorrect.
But if we multiply, any natural number by 2, we always get an even number.
Hence, two times a natural number is always even.
(iii) Given,
⇒ 3x + 1 > 4
⇒ 3x > 4 - 1
⇒ 3x > 3
⇒ x >
⇒ x > 1.
Hence, for x > 1, 3x + 1 > 4.
(iv) For any x ≥ 0, x3 ≥ 0.
(v) We know that,
A median is also the angle bisector in equilateral triangle.
Hence, in equilateral triangle, a median is also an angle bisector.
Answered By
1 Like
Related Questions
State whether the following statements are always true, always false or ambiguous. Justify your answers.
(i) There are 13 months in a year.
(ii) Diwali falls on a Friday.
(iii) The temperature in Magadi is 26°C.
(iv) The earth has one moon.
(v) Dogs can fly.
(vi) February has only 28 days.
State whether the following statements are true or false. Give reasons for your answers.
(i) The sum of the interior angles of a quadrilateral is 350°.
(ii) For any real number x, x2 ≥ 0.
(iii) A rhombus is a parallelogram.
(iv) The sum of two even numbers is even.
(v) The sum of two odd numbers is odd.
Use deductive reasoning to answer the following:
(i) Humans are mammals. All mammals are vertebrates. Based on these two statements, what can you conclude about humans?
(ii) Anthony is a barber. Dinesh had his hair cut. Can you conclude that Antony cut Dinesh’s hair?
(iii) Martians have red tongues. Gulag is a Martian. Based on these two statements, what can you conclude about Gulag?
(iv) If it rains for more than four hours on a particular day, the gutters will have to be cleaned the next day. It has rained for 6 hours today. What can we conclude about the condition of the gutters tomorrow?
(v) What is the fallacy in the cow’s reasoning in the cartoon below?

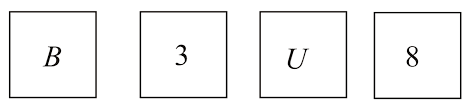
Once again you are given four cards. Each card has a number printed on one side and a letter on the other side. Which are the only two cards you need to turn over to check whether the following rule holds?
"If a card has a consonant on one side, then it has an odd number on the other side."