Mathematics
In a right angled triangle ABC, ∠ABC = 90°, D is mid-point of AC and AC = 13 cm. Calculate the length of BD.
Mid-point Theorem
3 Likes
Answer
6.5 cm
Reason
Draw DE || CB.
Since, DE || CB and AB is transversal,
∴ ∠AED = ∠ABC = 90° (Corresponding angles are equal)
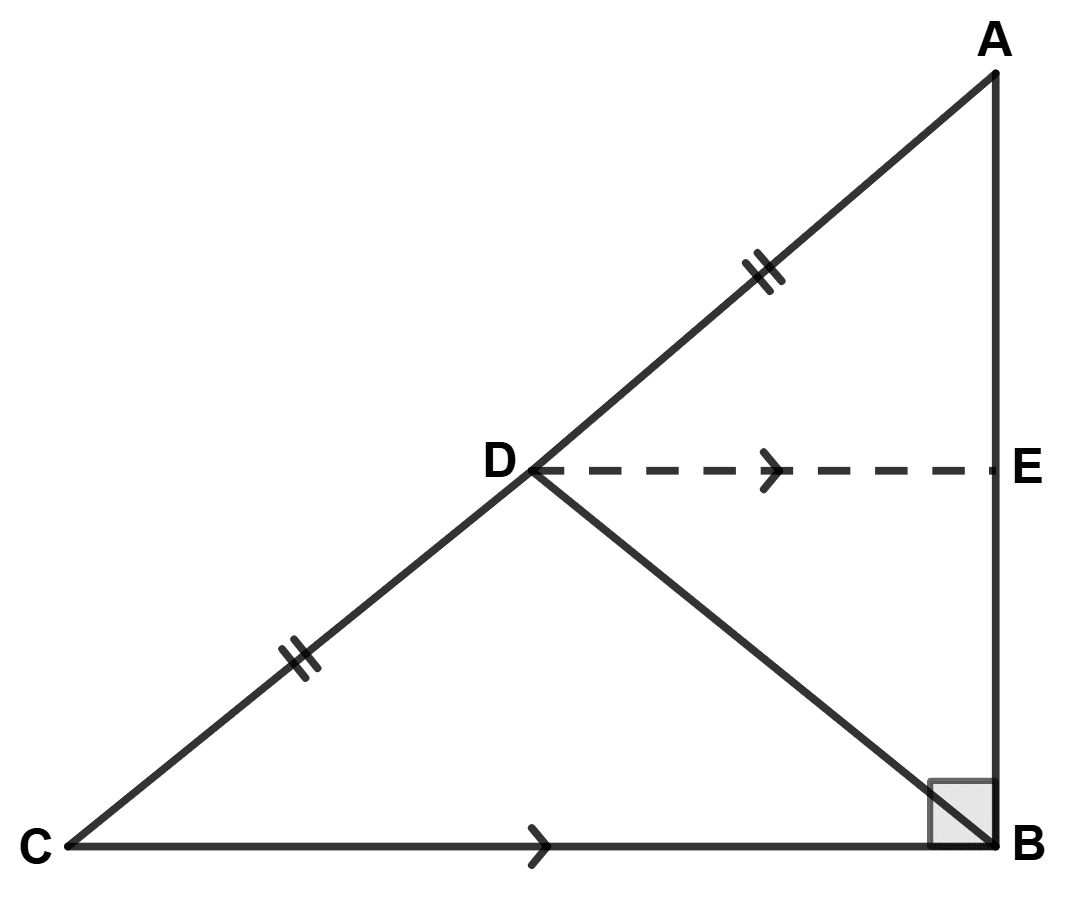
From figure,
⇒ ∠AED + ∠DEB = 180° (Since, AB is a straight line)
⇒ 90° + ∠DEB = 180°
⇒ ∠DEB = 180° - 90° = 90°.
As, D is mid-point of AC and DE is || CB.
∴ DE bisects AB (By converse of mid-point theorem)
∴ AE = BE.
In △ AED and △ BED,
⇒ ∠AED = ∠BED [Both equal to 90°]
⇒ AE = BE [Proved above]
⇒ DE = DE [Common side]
∴ △ AED ≅ △ BED [By S.A.S. axiom]
∴ BD = AD [By C.P.C.T.C.] ………….(1)
Given,
D is mid-point of AC.
∴ AD = ……..(2)
From equation (1) and (2), we get :
⇒ BD = = 6.5 cm
Answered By
1 Like
Related Questions
In the following figure, straight lines l, m and n are parallel to each other and G is the mid-point of CD. Find :
(i) BG, if AD = 12 cm
(ii) CF, if GE = 4.6 cm
(iii) AB, if BC = 4.8 cm
(iv) ED, if FD = 8.8 cm

Assertion (A): Using the information in the given figure, we have PQ = 10 cm.
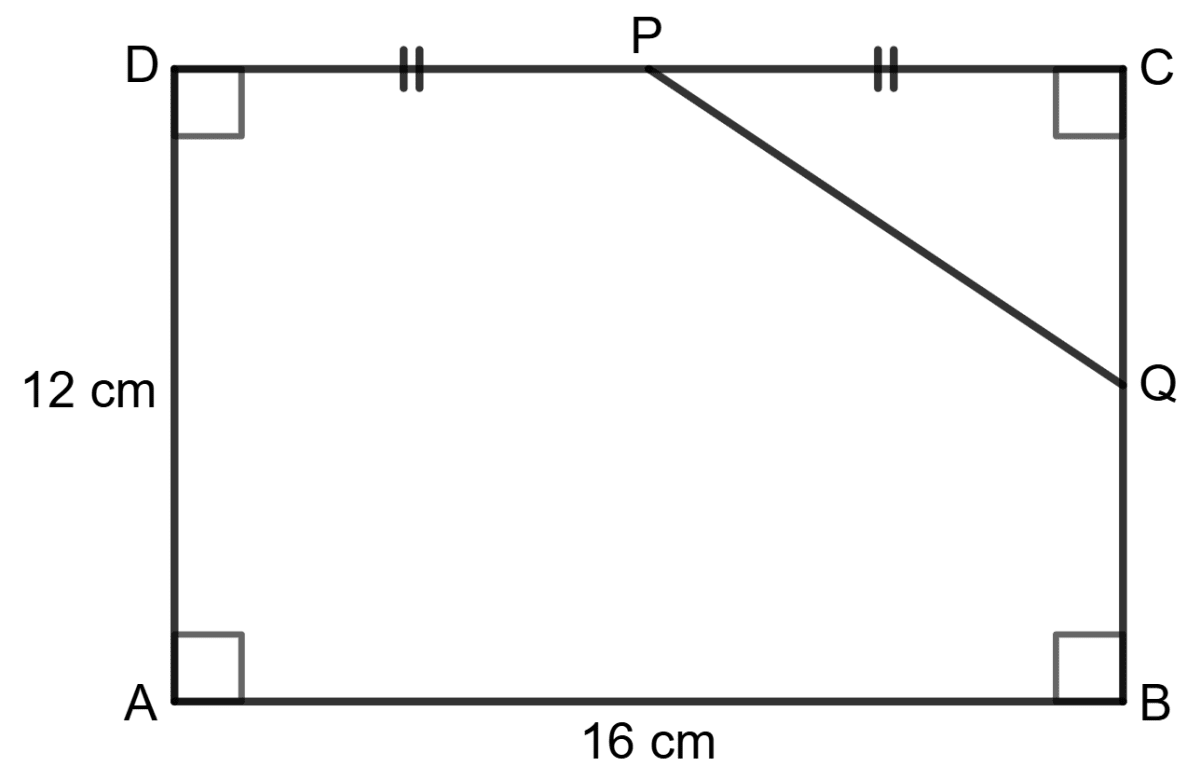
Reason (R): In right-triangle DAB, DB = 20 cm.

- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.