Mathematics
The slope of a line passing through (-1, 0) is 1.
Assertion (A): Its x-intercept and y-intercept are equal.
Reason (R): It makes an isosceles triangle with the coordinate axes.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Straight Line Eq
1 Like
Answer
By point-slope form,
⇒ y - y1 = m(x - x1)
Equation of line passing through (-1, 0) and slope = 1 is :
⇒ y - 0 = 1[x - (-1)]
⇒ y = x + 1
⇒ x - y + 1 = 0
In order to find x-intercept, substitute y = 0 in the equation of line :
⇒ x - 0 + 1 = 0
⇒ x = -1
In order to find y-intercept, substitute x = 0 in the equation of line :
⇒ 0 - y + 1 = 0
⇒ y = 1
Thus, x-intercept and y-intercept are not equal.
So, assertion (A) is false.
The triangle are formed with the axes has vertices : (0, 0), (-1, 0) and (0, 1).
By distance formula,
Distance between two points =
Since,two sides are equal in length. Therefore, it is an isosceles triangle.
So, reason (R) is true.
Thus, Assertion (A) is false, Reason (R) is true.
Hence, option 2 is the correct option.
Answered By
3 Likes
Related Questions
Which of the following equation represents a line equally inclined to the axes ?
2x - 3y + 7 = 0
x - y = 7
x = 7
y = -7
y = -2 is the equation of a line.
Assertion (A): Its x-intercept is zero.
Reason (R): It does not intersect x-axis.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Given below are the equation of two lines:
y = 2x + 8 and y =
Assertion (A): The two lines are perpendicular to each other.
Reason (R): Their slopes are reciprocal of each other.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
l and m are two lines in the figure given below:
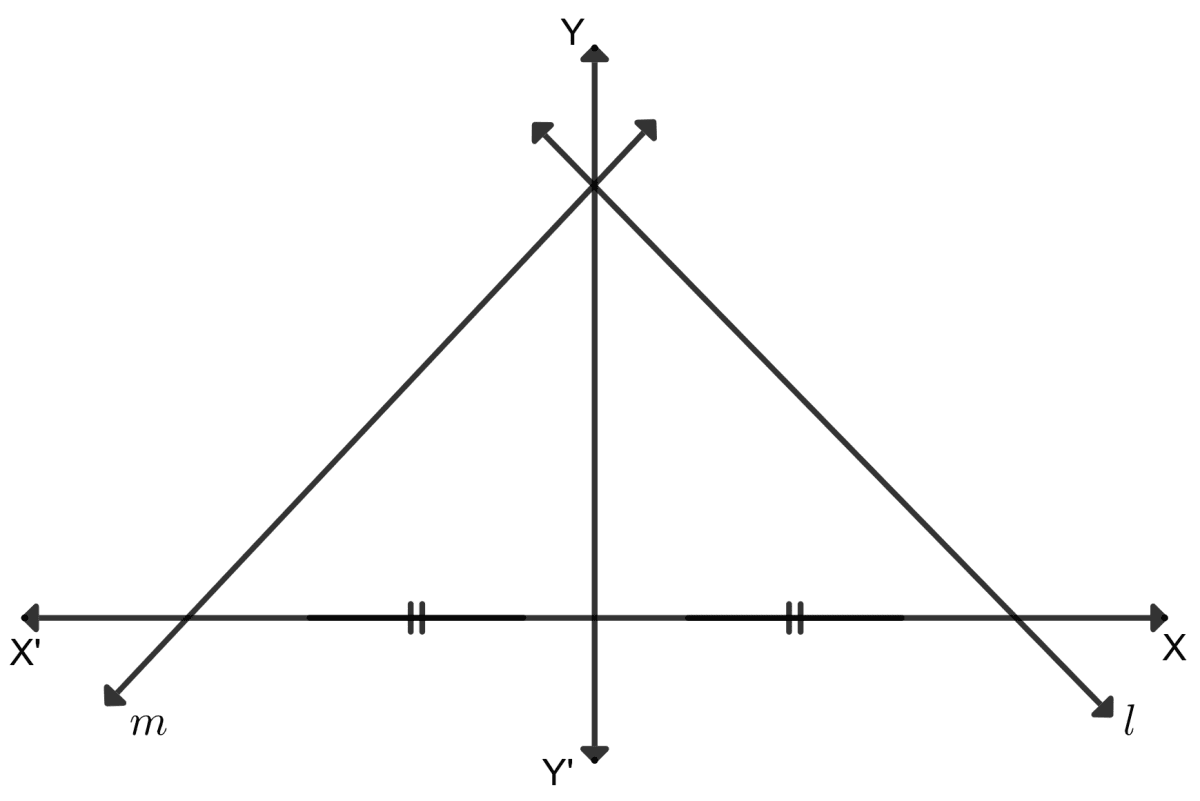
Assertion (A): They have equal y-intercept.
Reason (R): Their inclination is same.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).