Solve the following system of equations by using the method of cross multiplication:

$\dfrac{10}{x + y} + \dfrac{2}{x - y} = 4, \dfrac{15}{x + y} - \dfrac{5}{x - y} + 2 = 0$, where x ≠ -y and x ≠ y

Substituting $\dfrac{1}{x + y}= a, \dfrac{1}{x - y} = b$ in $\dfrac{10}{x + y} + \dfrac{2}{x - y} = 4$, we get:

⇒ 10a + 2b = 4

⇒ 10a + 2b - 4 = 0     …..(1)

Substituting $\dfrac{1}{x + y}= a, \dfrac{1}{x - y} = b$ in $\dfrac{15}{x + y} - \dfrac{5}{x - y} + 2 = 0$, we get:

⇒ 15a - 5b + 2 = 0     ….(2)

Applying cross-multiplication method for solving equations (1) and (2), we get :

$\Rightarrow \dfrac{a}{(2) \times (2) - (-5) \times (-4)} = \dfrac{b}{(-4) \times (15) - (2) \times (10)} = \dfrac{1}{(10) \times (-5) - (15) \times (2)} \\[1em] \Rightarrow \dfrac{a}{(4) - 20} = \dfrac{b}{-60 - 20} = \dfrac{1}{-50 - 30} \\[1em] \Rightarrow \dfrac{a}{-16} = \dfrac{b}{-80} = \dfrac{1}{-80} \\[1em] \Rightarrow \dfrac{a}{-16} = \dfrac{1}{-80} \text{ and } \dfrac{b}{-80} = \dfrac{1}{-80} \\[1em] \Rightarrow a = \dfrac{-16}{-80} \text{ and } b = \dfrac{-80}{-80} \\[1em] \Rightarrow a = \dfrac{1}{5} \text{ and } b = 1.$

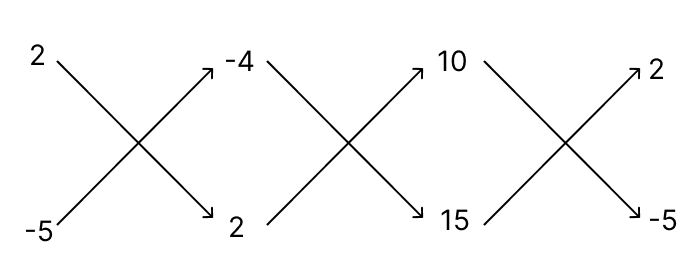
Now we have a = $\dfrac{1}{5}$ and b = 1,

$\Rightarrow \dfrac{1}{x + y} = a \\[1em] \Rightarrow \dfrac{1}{x + y} = \dfrac{1}{5} \\[1em] \Rightarrow x + y = 5 \text{ ……….(3)} \\[1em] \Rightarrow \dfrac{1}{x - y} = b \\[1em] \Rightarrow \dfrac{1}{x - y} = 1 \\[1em] \Rightarrow x - y = 1 \text{ ……..(4)}$

On adding equations (3) and (4) we get,

⇒ (x + y) + (x - y) = 5 + 1

⇒ 2x = 6

⇒ x = $\dfrac{6}{2} = 3$.

Substituting value of x in equation (4) we get,

⇒ x - y = 1

⇒ 3 - y = 1

⇒ y = 3 - 1 = 2.

Hence, x = 3, y = 2.