Mathematics
Statement 1: The point P(x, y) is at a distance of 6 unit from origin, then P lies in the first quadrant.
Statement 2: Point P can lie in any quadrant.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Distance Formula
1 Like
Answer
Given, the point P(x, y) is at a distance of 6 unit from origin.
By distance formula,
Distance between two points =
The above equation defines a circle centered at the origin with radius 6. That circle covers all four quadrants, so P can lie anywhere on that circle, not necessarily in the first quadrant.
∴ Statement 1 is false, and statement 2 is true.
Hence, option 4 is the correct option.
Answered By
1 Like
Related Questions
AB (= 10 unit) is diameter of a circle with center at point P = (x, 0) and point B = (0, y). The relation between x and y is:
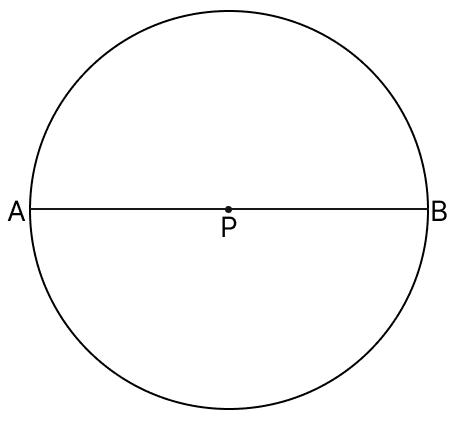
x + y = 10
x + y = 25
x2 + y2 = 5
x2 + y2 = 25
Statement 1: For the point P, x = -4 and y = 3, the distance of P from origin is 3 + 4 = 7.
Statement 2: P = (-4, 3) and its distance from origin = .
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): If A = (2x, y), B(x, 2y) and AB = 5 unit, then x + y = 5.
Reason (R): = 5
⇒ x2 + y2 = 25
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Assertion (A): The distance between the points A(x, 2x) and B(x, 0) is 4 unit, the point B is (2, 0).
Reason (R): = 2
⇒ x2 = 4 and x = ± 2
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.