Mathematics
The diagonal of a cube is m. Find its surface area.
Surface Area, Volume, Capacity
38 Likes
Answer
Given:
The diagonal of a cube = m
Let s be the side of cube.
As we know that the diagonal of the cube = x side
As we know, the surface area of cube = 6 x side2
= 6 x (25)2 m2
= 6 x 625 m2
= 3,750 m2
Hence, the surface area of the cube is 3,750 m2.
Answered By
24 Likes
Related Questions
Four cubes, each of edge 9 cm, are joined as shown below :
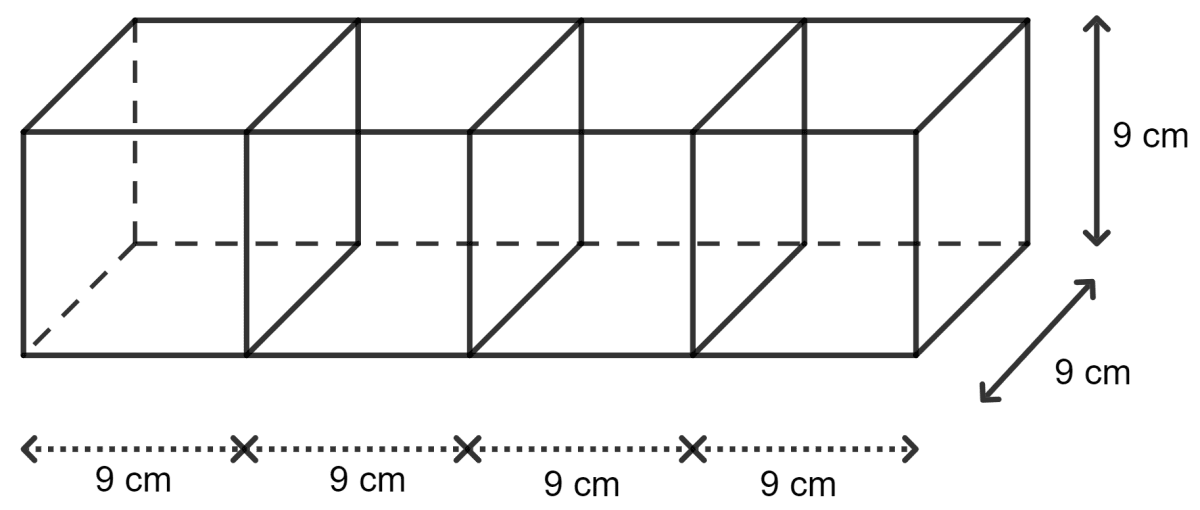
Write the dimensions of the cuboid obtained. Also, find total surface area and volume.
What is the maximum length of a rod which can be kept in a rectangular box with internal dimensions 32 cm x 24 cm x 8 cm.
A rectangular room is 4.5 m long, 4 m wide and 3 m high. Find the cost of white washing its walls and the roof at ₹ 15 per square metre.
The dimensions of a hall are 40 m x 25 m x 5 m. The number of persons which can be accommodated in the hall is (each person requires 5 m3 of air) :
1000
2000
5000
2500