The figure given below shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B : ∠C : ∠D = 5 : 6 : 7.

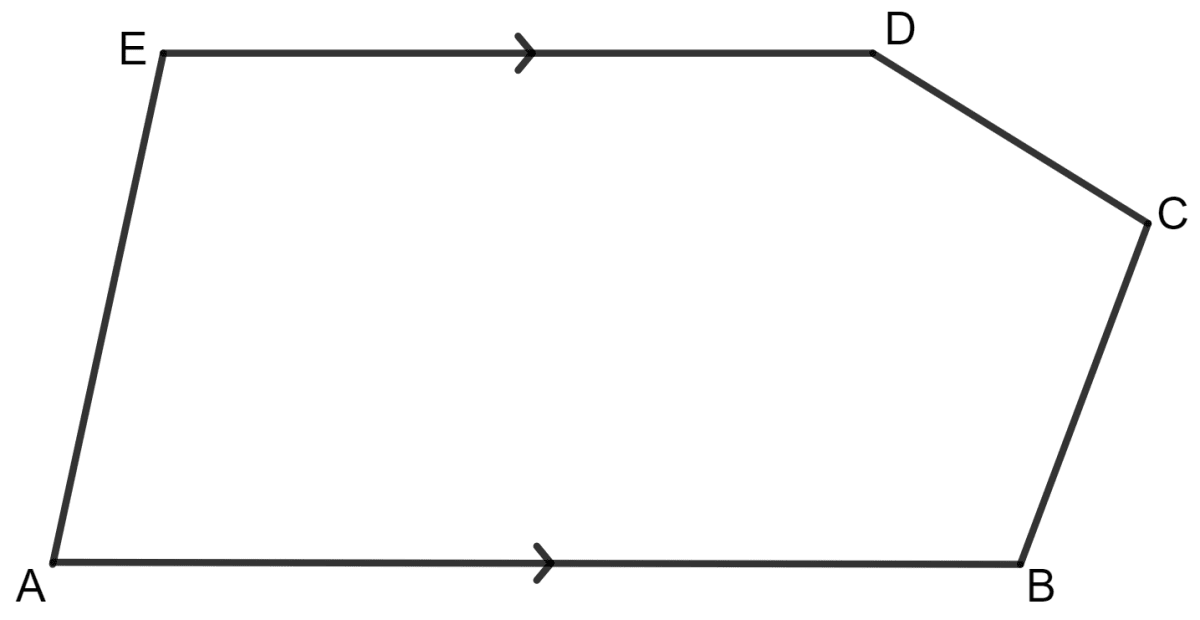
(i) Using formula, find the sum of interior angles of the pentagon.

(ii) Write the value of ∠A + ∠E.

(iii) Find angles B, C and D.

(i) According to the properties of polygons, if a polygon has n sides, then the sum of its interior angles is (2n - 4) x 90°.

A pentagon has 5 sides.

So, the sum of its interior angles is:

(2 x 5 - 4) x 90°

= (10 - 4) x 90°

= 6 x 90°

= 540°

Hence, the sum of the interior angles of a pentagon is 540°.

(ii) It is given that in pentagon ABCDE, sides AB and ED are parallel to each other.

As we know, corresponding angles are formed when a transversal crosses two parallel lines, and the sum of corresponding angles is 180°.

Hence, ∠A + ∠E = 180°.

(iii) It is given that ∠B : ∠C : ∠D = 5 : 6 : 7.

Let the common factor of the angles be a. So, ∠B = 5a, ∠C = 6a and ∠D = 7a.

Therefore,

⇒ ∠A + ∠B + ∠C + ∠D + ∠E = 540°

⇒ ∠A + 5a + 6a + 7a + ∠E = 540°

⇒ ∠A + ∠E + 18a = 540°

Since the sum of all angles in a pentagon is 540° and we know ∠A + ∠E equals 180°.

⇒ 180° + 18a = 540°

⇒ 18a = 540° - 180°

⇒ 18a = 360°

⇒ a = $\dfrac{360°}{18}$

⇒ a = 20°

Thus,

∠B = 5a = 5 x 20° = 100°

∠C = 6a = 6 x 20° = 120°

∠D = 7a = 7 x 20° = 140°

Hence, ∠B = 100°, ∠C = 120° and ∠D = 140°.