Mathematics
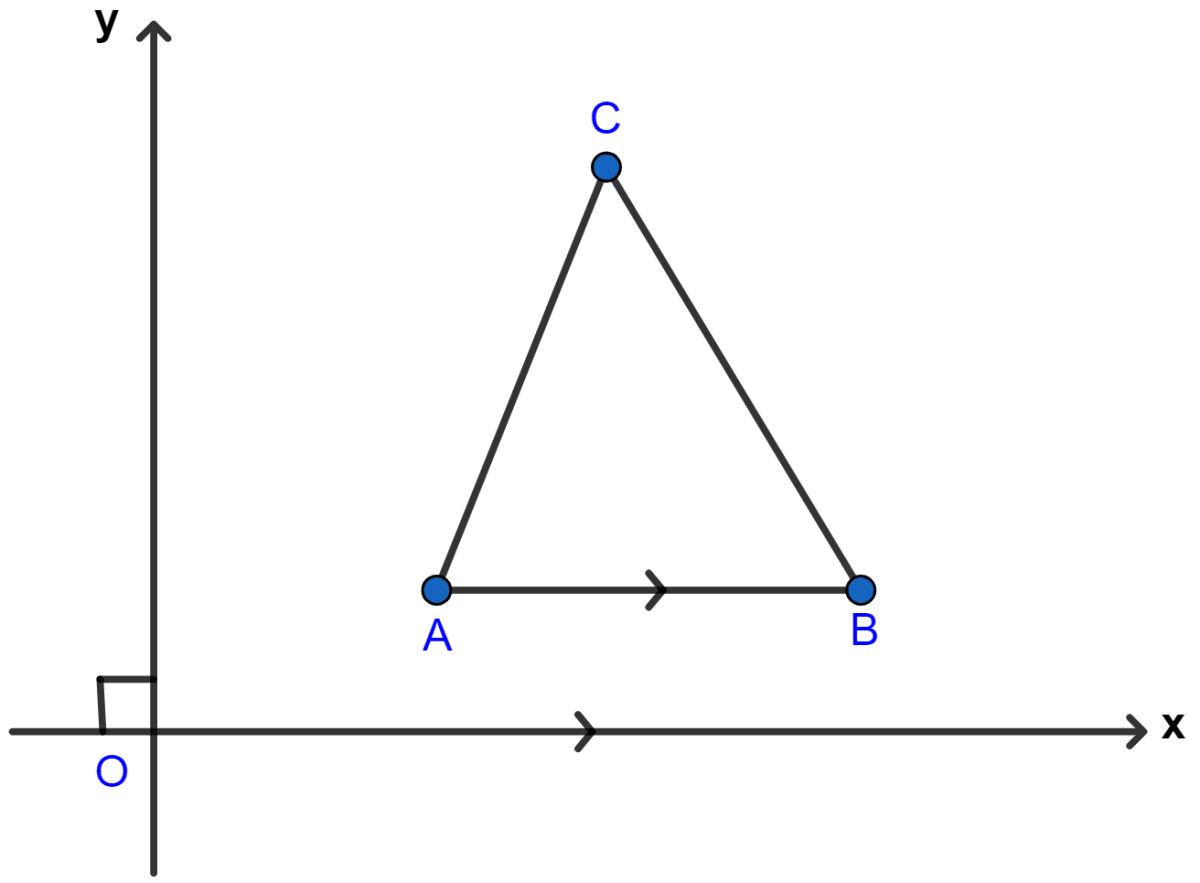
The side AB of an equilateral triangle ABC is parallel to the x-axis. Find the slopes of all its sides.
Straight Line Eq
8 Likes
Answer
Since, AB is parallel to x-axis. It's slope will be equal to the slope of x-axis.
Slope of AB = 0.
We know that,
Angle in equilateral triangle = 60°.
So,
AC is inclined at an angle of 60° from AB so also from x-axis. (As AB || x-axis).
Slope of AC = tan 60° = .
BC is inclined at angle of (180° - 60°) = 120°.
Slope of BC = tan 120° = -.
Hence, slopes of sides of triangle ABC = 0, .
Answered By
8 Likes
Related Questions
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find :
(i) equation of line AB.
(ii) equation of line CD.
(iii) co-ordinates of point E and D.

Find the equation of the line through the points A(-1, 3) and B(0, 2). Hence, show that the points A, B and C(1, 1) are collinear.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
(i) Write the co-ordinates of A.
(ii) Find the length of AB and AC.
(iii) Find the ratio in which Q divides AC.
(iv) Find the equation of the line AC.
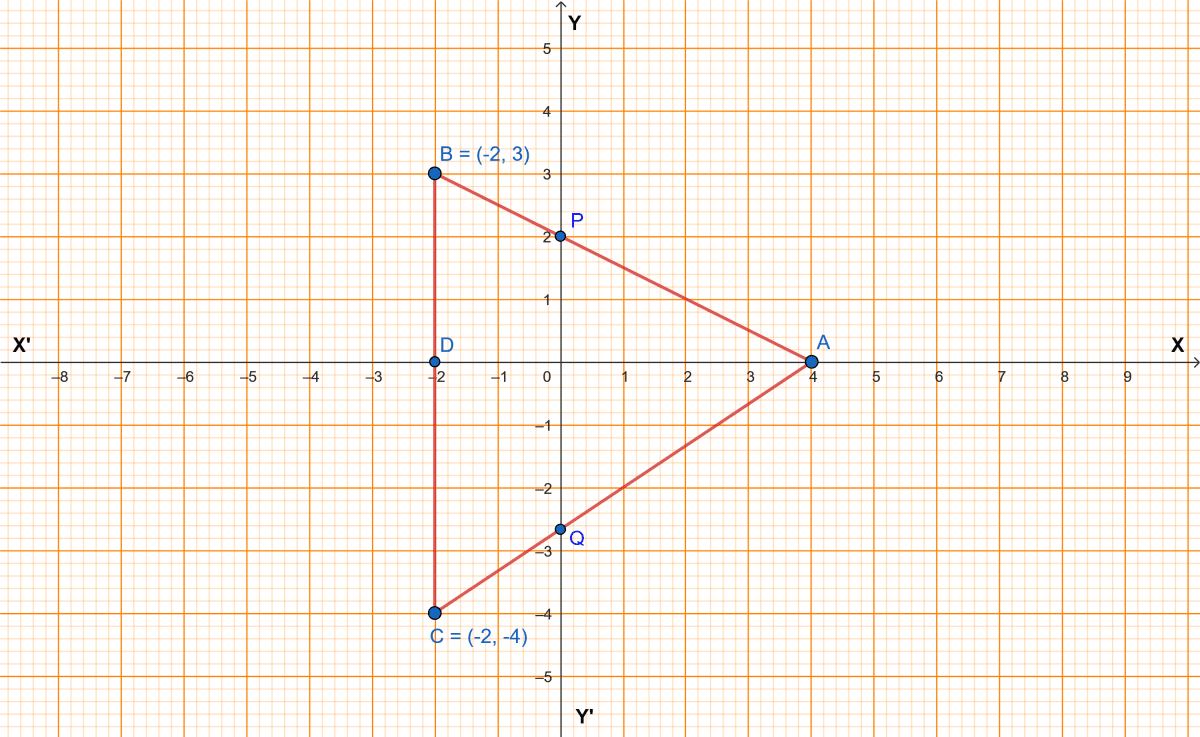
A line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ratio 1 : 2.
(i) Find the co-ordinates of A and B.
(ii) Find the equation of the line through P and perpendicular to AB.
