Mathematics
The sum of interior angles of a regular polygon is thrice the sum of its exterior angles. Find the number of sides in the polygon.
Geometrical Shapes
3 Likes
Answer
It is given that the sum of the interior angles of a regular polygon is thrice the sum of its exterior angles.
Let the exterior angle of the polygon be a.
Then the interior angle is 3a.
As we know, the sum of the interior angle and the exterior angle is 180°.
⇒ a + 3a = 180°
⇒ 4a = 180°
⇒ a =
⇒ a = 45°
So, the exterior angle is 45°.
The interior angle is 3a = 3 x 45° = 135°.
Each interior angle of a regular polygon can be calculated using the formula:
⇒ 135° =
By cross multiplying, we get
⇒ 135°n = (2n - 4) 90°
⇒ 135°n = 180°n - 360°
⇒ 180°n - 135°n = 360°
⇒ 45°n = 360°
⇒ n =
⇒ n = 8
Hence, the number of sides is 8.
Answered By
2 Likes
Related Questions
In quadrilateral ABCD, sides AB and DC are parallel to each other. If ∠A : ∠D = 2 : 3 and ∠B : ∠C = 7 : 8; find all the angles of quadrilateral ABCD.
In quadrilateral ABCD; 2∠A = 3∠B = 2∠C = 6∠D. Find all the angles of the quadrilateral.
Angles of a quadrilateral are (4x)°, 5(x + 2)°, (7x - 20)° and 6(x + 3)°. Find:
(i) the value of x.
(ii) each angle of the quadrilateral.
Use the information given in the following figure to find:
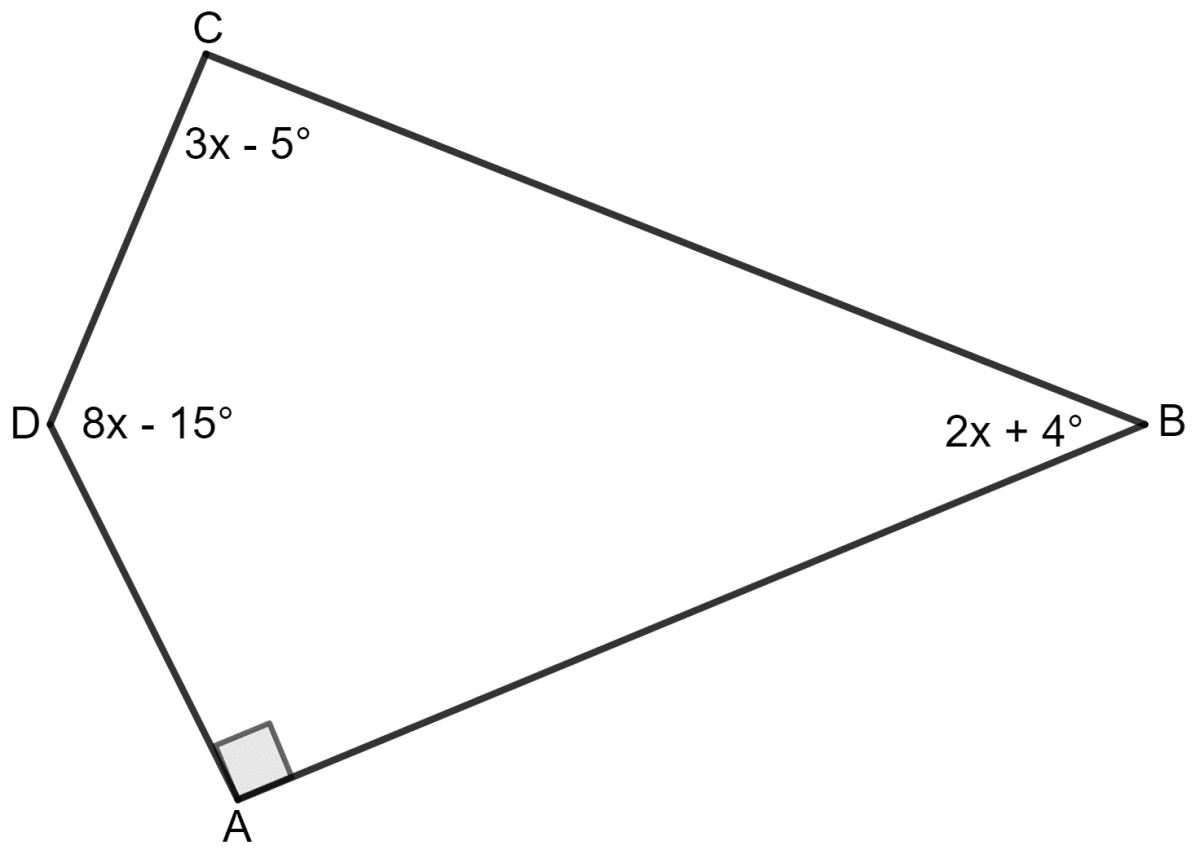
(i) x.
(ii) ∠B and ∠C.