Physics
Three identical bulbs B1, B2 and B3 each of power rating 18 W, 12 V are connected to a battery of 12 V.
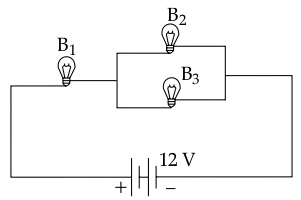
(a) Calculate :
- the resistance of each bulb
- the current drawn from the cell
(b) If the bulb B3 is removed from the circuit, then will the brightness of the bulb B1 increase, decrease or remain the same?
Current Electricity
8 Likes
Answer
Given,
Battery emf (ε) = 12 V
Voltage rating of eac bulb (V) = 12 V
Power rating of eac bulb (P) = 18 W
(a)
- Let resistance of each bulb be R.
Then,
- As, B2 and B3 are in parallel combination then
Here, R1 = R2 = 8 Ω
Now this combination is in series with B1 then
RS = RP + R = 4 + 8 = 12 Ω
So,
Hence, current drawn from the battery is 1 A.
(b) When B3 is removed, the circuit becomes :
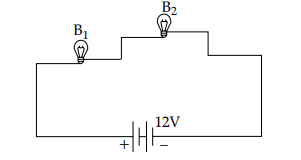
Now, the equivalent resistance = 8 + 8 = 16 Ω.
Since, the resistance increases, current in the circuit decreases.
Hence, brightness of B1 decreases.
Answered By
4 Likes
Related Questions
The diagram shows wiring in a meter room of a building.
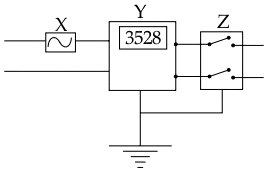
(a) What is the current rating of device X?
(b) What is the difference between the switch Z shown in the diagram and the switches you use to operate different appliances at home?
(c) What is the unit of the physical quantity displayed in Y?
Study the diagram given below and answer the questions that follow :
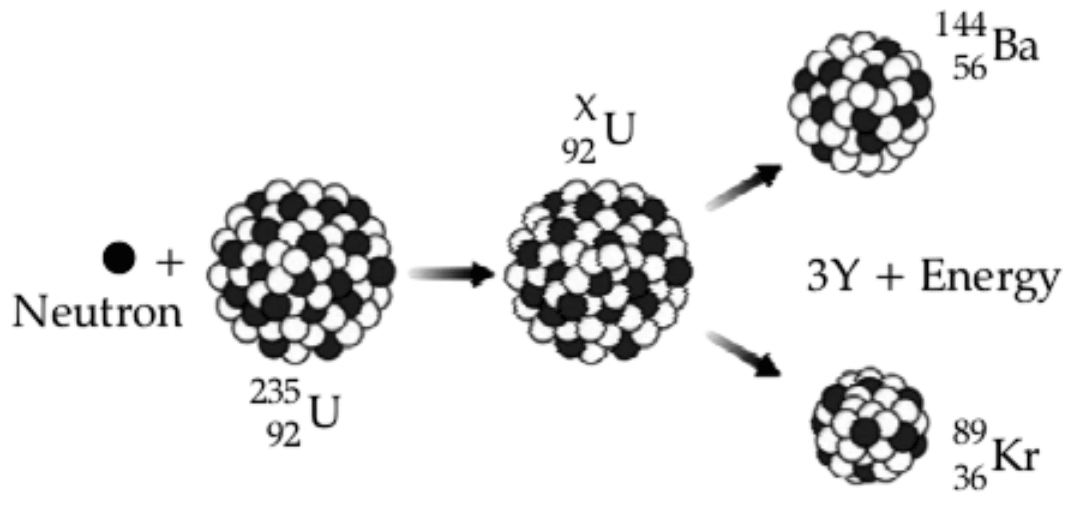
(a) Name the process depicted in the diagram.
(b) What is the value of X?
(c) Identify Y, the missing product of the reaction.
30 g of ice at 0°C is used to bring down the temperature of a certain mass of water at 70°C to 20°C. Find the mass of water.
[Specific heat capacity of water = 4.2 J g⁻¹ °C⁻¹ and specific latent heat of ice = 336 J g⁻¹]
(a) A certain amount of heat will warm 1 g of material X by 10°C and 1 g of material Y by 40°C. Which material has higher specific heat capacity?
(b) Which material, X or Y, would you select to make a calorimeter?
(c) The specific heat capacity of a substance remains the same when it changes its state from solid to liquid. State True or False.