Mathematics
Through any point in the bisector of an angle a straight line is drawn parallel to either arm of the angle. Prove that the triangle so formed is isosceles.
Triangles
11 Likes
Answer
From figure,
AL is the bisector of angle A. Let D be any point on AL. From D, a straight line DE is drawn parallel to AC.
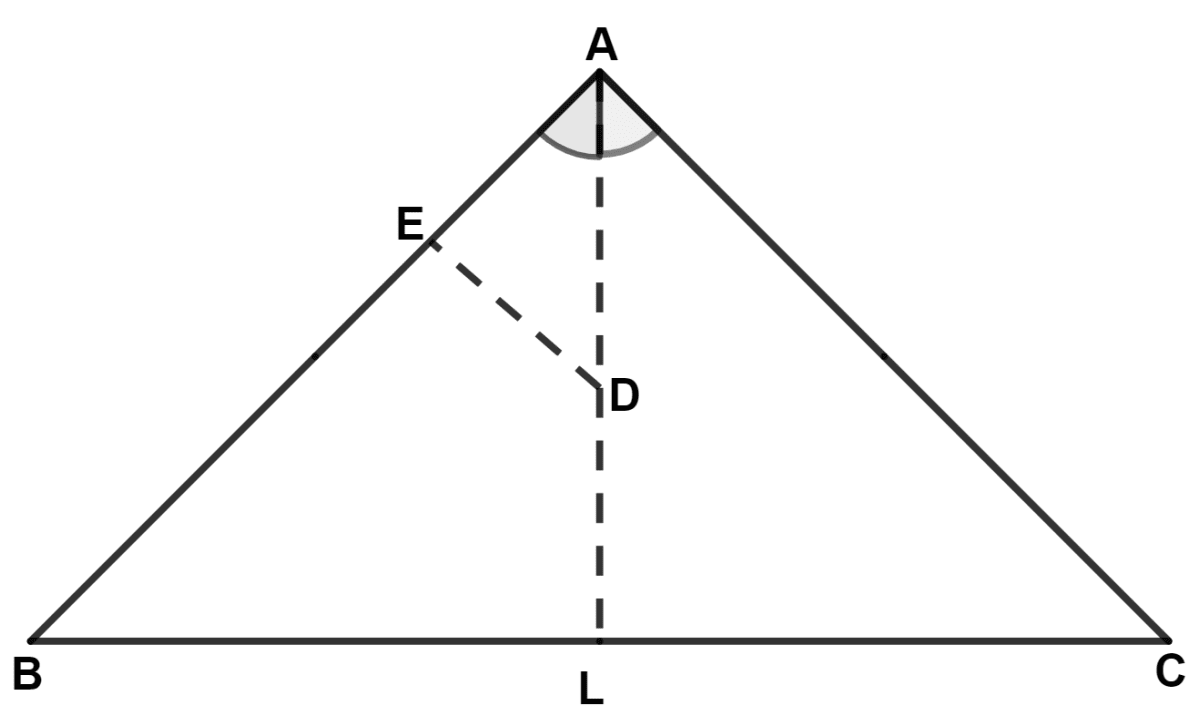
DE || AC
⇒ ∠ADE = ∠DAC (Alternate angles are equal) …….(1)
⇒ ∠DAC = ∠DAE (As, AL is the bisector of ∠A) ……(2)
From equation (1) and (2), we get :
⇒ ∠ADE = ∠DAE.
∴ AE = ED (Sides opposite to equal angles are equal)
∴ AED is an isosceles triangle.
Hence, proved that triangle formed is isosceles triangle.
Answered By
7 Likes
Related Questions
In quadrilateral ABCD, side AB is the longest and side DC is the shortest. Prove that :
(i) ∠C > ∠A
(ii) ∠D > ∠B
In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : ∠ADC is greater than ∠ADB.
In isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that :
(i) AC > AD
(ii) AE > AC
(iii) AE > AD
Given : ED = EC
Prove : AB + AD > BC.