Mathematics
In a trapezium ABCD, AB and CD are parallel sides of length 10 cm and 15 cm respectively. Calculate the length of the line joining the mid-points of two non-parallel sides.
Mid-point Theorem
1 Like
Answer
12.5 cm
Reason
Let E and F be midpoints of AD and BC, respectively.
Join diagonal BD.
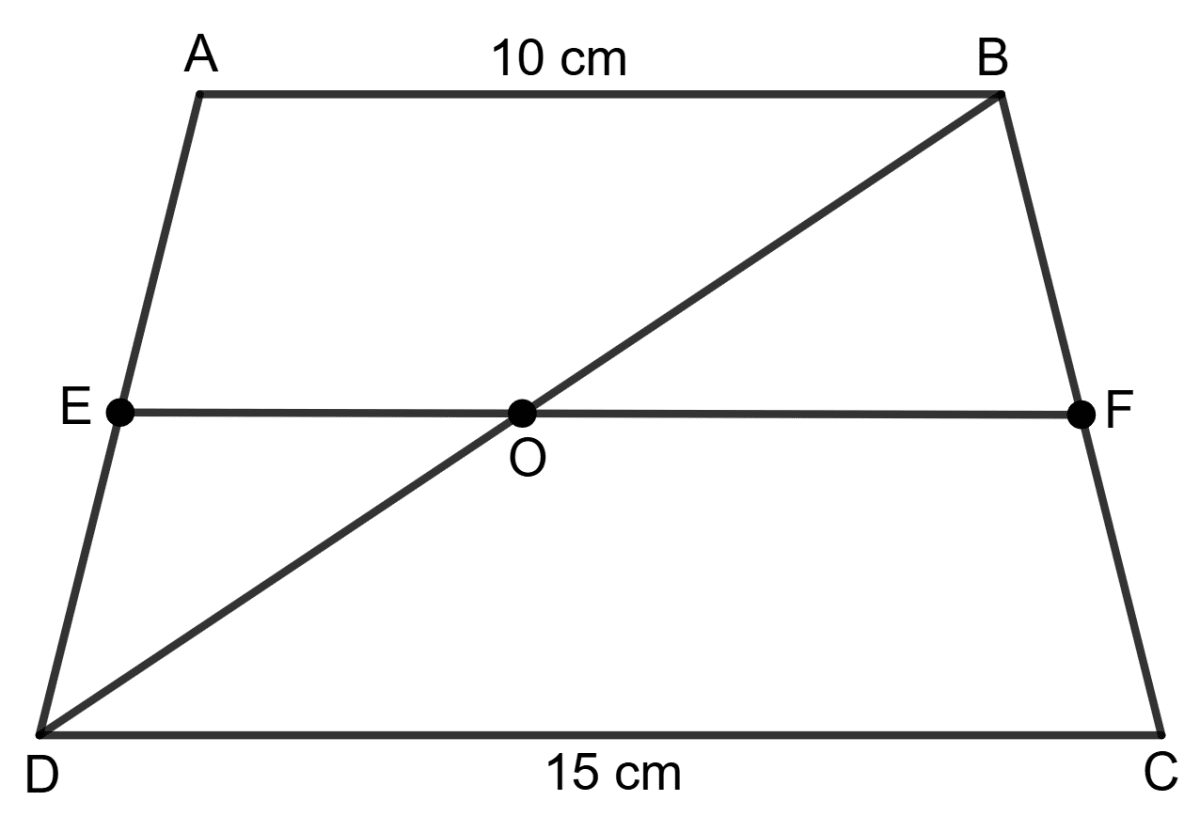
In a trapezium, line joining midpoints of non-parallel sides is parallel to the parallel sides,
∴ AB || EF || DC
In Δ ABD, E is mid point of AD and EO || AB. By mid-point theorem,
EO = AB …………….(1)
In Δ BDC, F is mid point of BC and OF || DC. By mid-point theorem,
OF = DC …………….(2)
From the figure,
EF = EO + OF
= AB + DC
= (AB + DC)
= cm
= cm
= 12.5 cm
Answered By
1 Like
Related Questions
ABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that :
(i) D is mid-point of AC.
(ii) MD is perpendicular to AC.
(iii) CM = MA = AB
In the following figure, l // m // n. If OC = OD = 5 cm, OA = 8cm and OE = 10 cm, find OB and OF.

Assertion (A): Using the information in the given figure, we get CE : EA = 5:3.
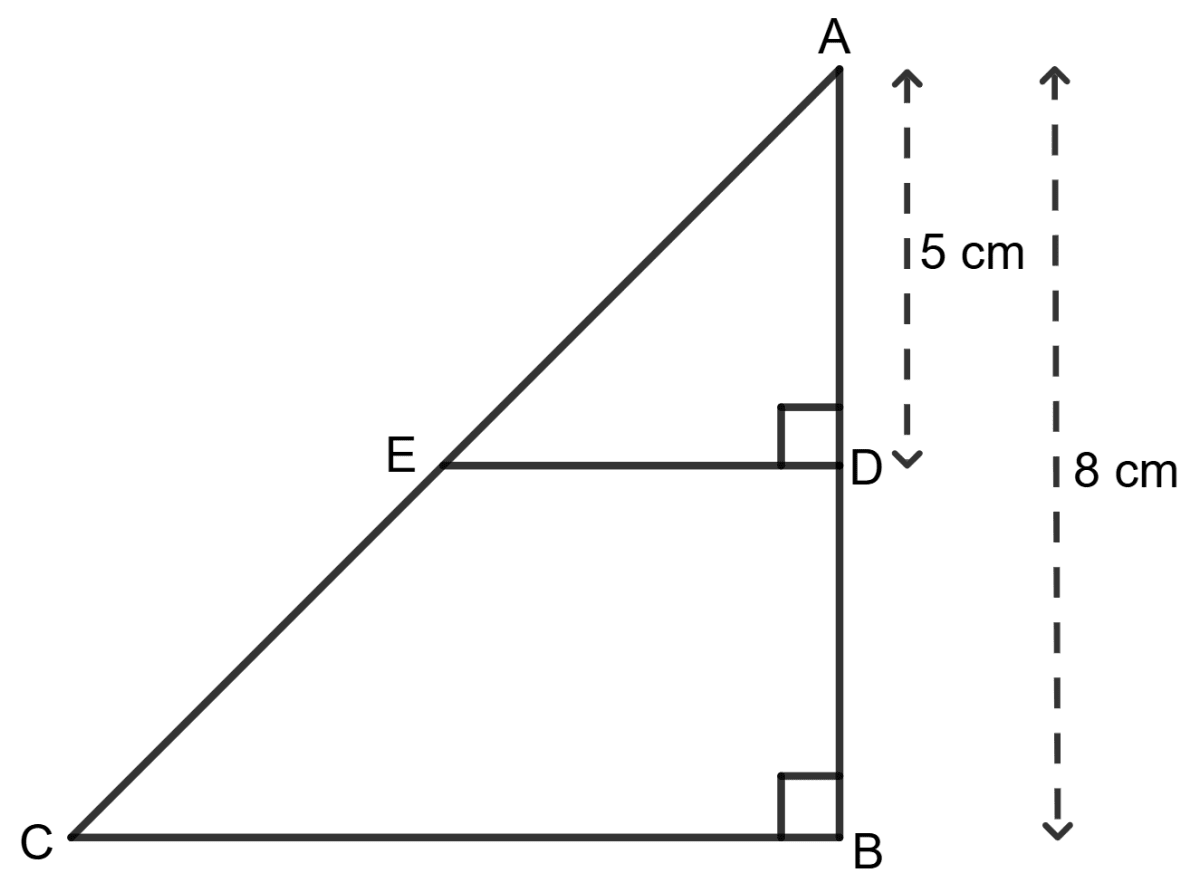
Reason (R): Since, ∠ADE = ∠ABC = 90°
so,
⇒ CE : EA = 3 : 5
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.