In triangle PQR, the medians QS and RT are produced to points U and W respectively such that SU = QS and WT = TR.

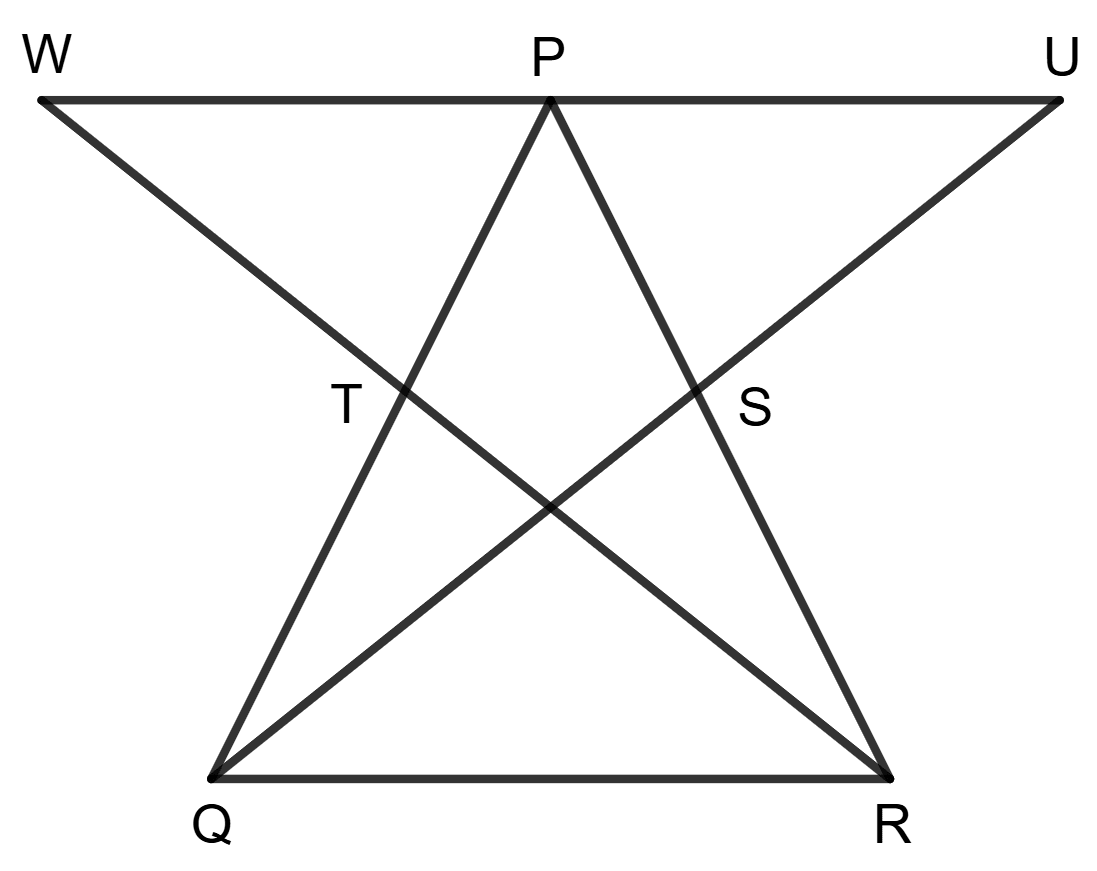
Which of the following statement/s is/are true ?

A ⇒ W, P and U are collinear

B ⇒ P is the mid-point of WU

C ⇒ TS = $\dfrac{1}{2}$ QR

A, B and C are correct

Reason

Given,

⇒ SU = QS

∴ S is the mid-point of QU.

⇒ WT = TR

∴ T is the mid-point of WR.

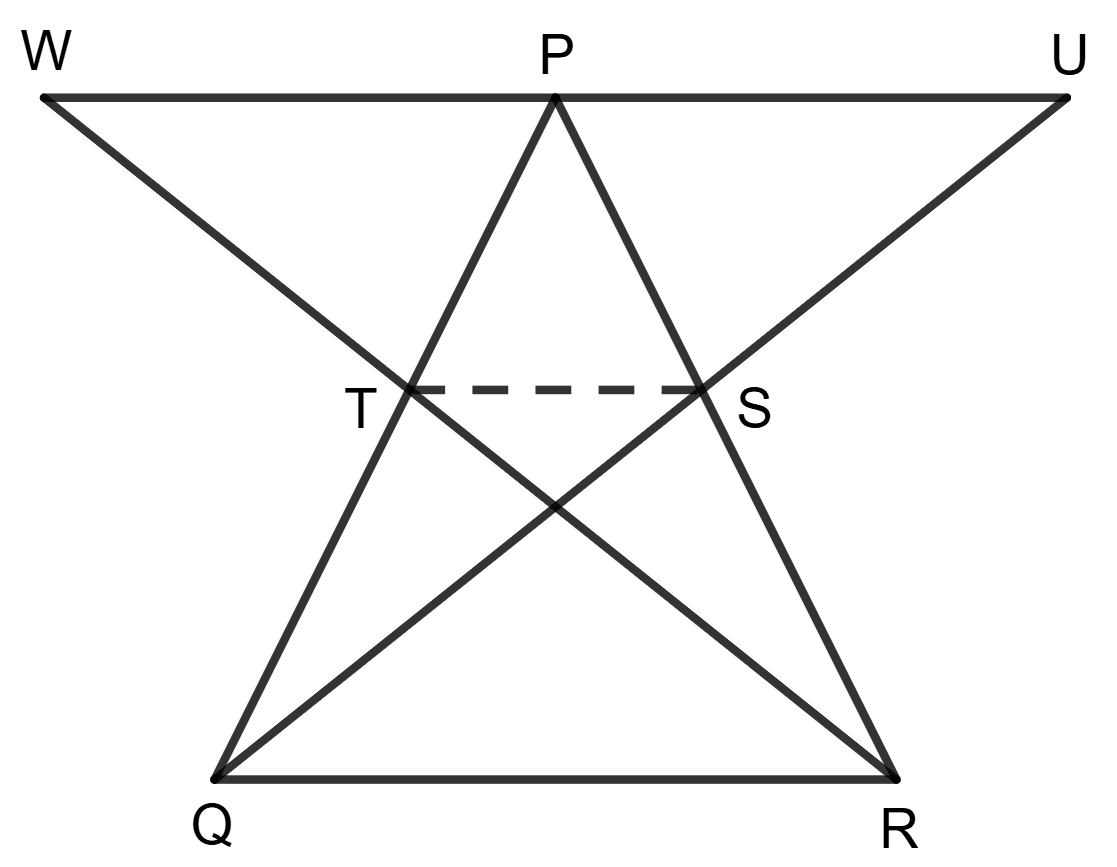
In Δ PQU,

T is the mid-point of PQ (as RT is the median) and S is the mid-point of QU.

∴ TS = $\dfrac{1}{2}PU$ and TS || PU [By mid-point theorem]

In Δ PRW,

S is the mid-point of PR (as QS is the median) and T is the mid-point of WR.

∴ TS = $\dfrac{1}{2}WP$ and TS || WP [By mid-point theorem]

Since, TS || PU and TS || WP,

Thus, PU and WP lie along same straight line as both PU and WP pass through same point P and is parallel to same line TS.

Thus, W, P and U are collinear.

So, statement A is correct.

As, TS = $\dfrac{1}{2}WP$ and TS = $\dfrac{1}{2}PU$

∴ $\dfrac{1}{2}WP = \dfrac{1}{2}PU$

⇒ WP = PU

∴ P is the mid-point of WU.

So, statement B is correct.

In △ PQR,

T is midpoint of PQ and S is midpoint of PR. Using the midpoint-theorem,

TS ∥ QR and TS = $\dfrac{1}{2}$ QR

So, statement C is correct.