Mathematics
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
Circles
4 Likes
Answer
Let O and O' be the centres of two intersecting circles, where points of the intersection are P and Q and PA and PB are their diameters respectively.
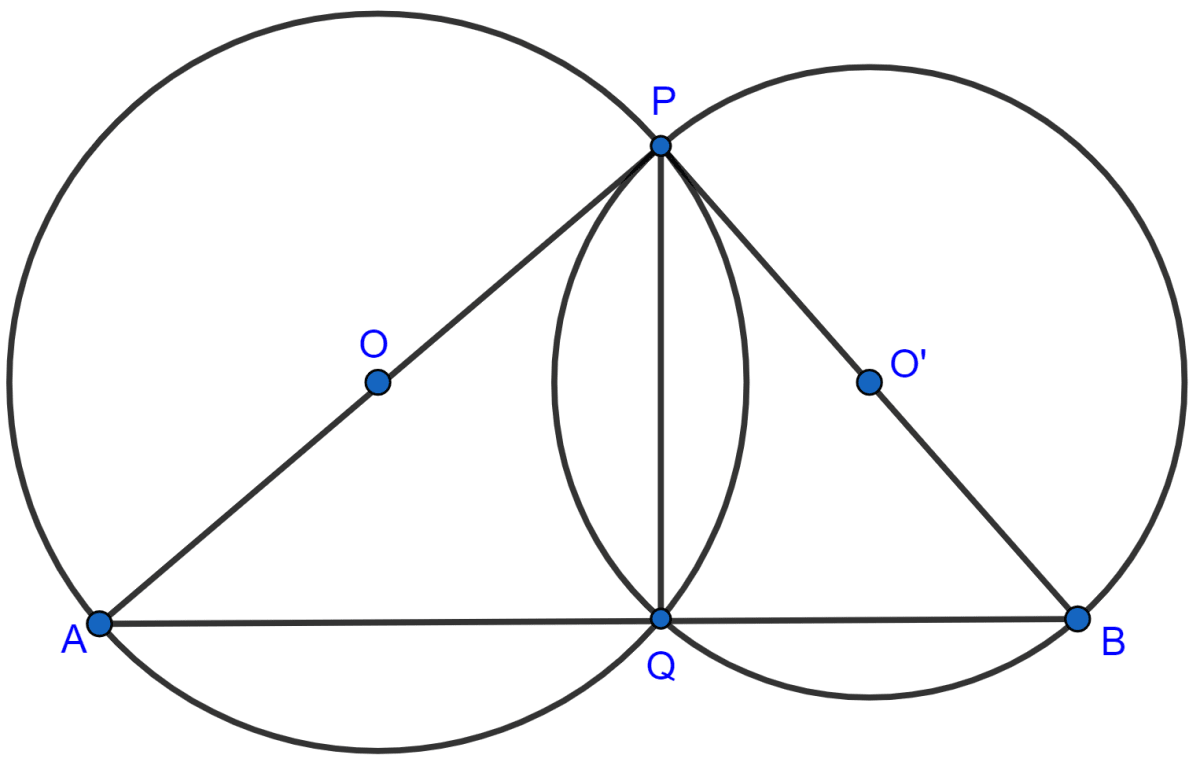
As angle in a semicircle is a right angle.
∴ ∠AQP = 90° and ∠BQP = 90°
Adding,
⇒ ∠AQP + ∠BQP = 180°
⇒ ∠AQB = 180°.
Hence, the points A, Q and B are collinear.
Answered By
3 Likes
Related Questions
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED

In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD