Mathematics
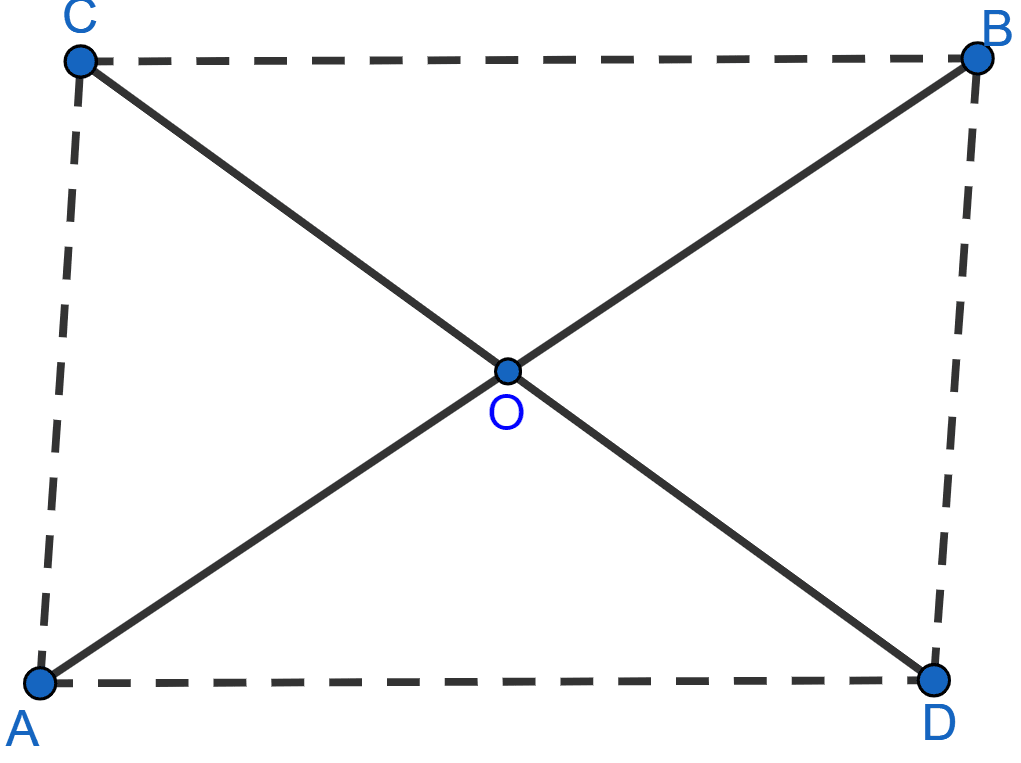
Two line segments AB and CD bisect each other at O. Prove that
(i) AC = BD
(ii) ∠CAB = ∠ABD
(iii) AD || CB
(iv) AD = CB
Triangles
121 Likes
Answer
(i) Given, AB and CD bisect each other at O.
∴ OC = OD and OA = OB
∠COA = ∠BOD (Vertically opposite angles).
∴ △COA ≅ △BOD by SAS axiom.
We know that corresponding sides of congruent triangles are equal.
Hence, AC = BD.
(ii) As, △COA ≅ △BOD we know that corresponding angles of congruent triangles are equal.
∠CAO = ∠OBD …..(i)
From figure we get,
∠CAO = ∠CAB and ∠OBD = ∠ABD.
Substituting above values in (i) we get,
∠CAB = ∠ABD.
Hence, proved that ∠CAB = ∠ABD.
(iii) From figure,
OC = OD and OA = OB
∠AOD = ∠BOC (Vertically opposite angles).
∴ △COB ≅ △AOD by SAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ ∠BCO = ∠ADO and ∠CBO = ∠OAD.
Since, ∠BCO, ∠ADO and ∠CBO, ∠OAD are alternate angles,
∴ AD || CB.
Hence, proved that AD || CB.
(iv) Given, AB and CD bisect each other at O.
∴ OC = OD and OA = OB
∠AOD = ∠BOC (Vertically opposite angles).
∴ △AOD ≅ △BOC by SAS axiom.
We know that corresponding parts of congruent triangles are equal.
Hence, AD = CB.
Answered By
63 Likes
Related Questions
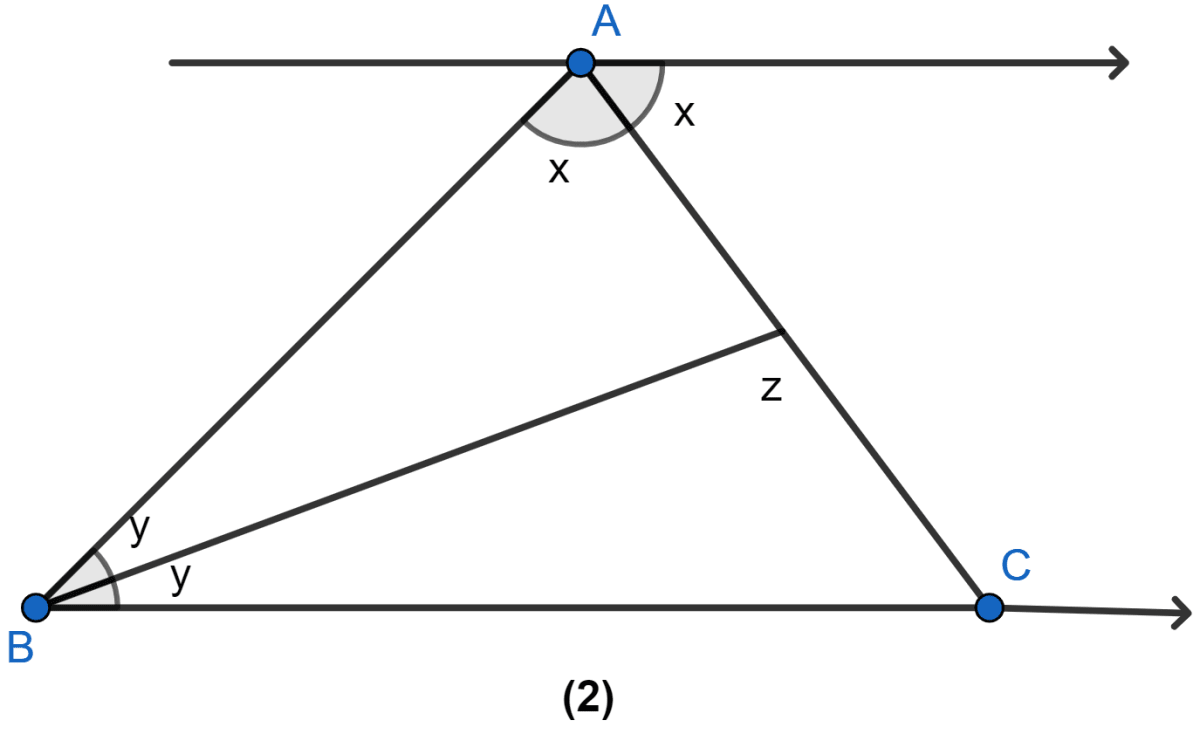
In the figure (2) given below, prove that
(i) x + y = 90°
(ii) z = 90°
(iii) AB = BC.
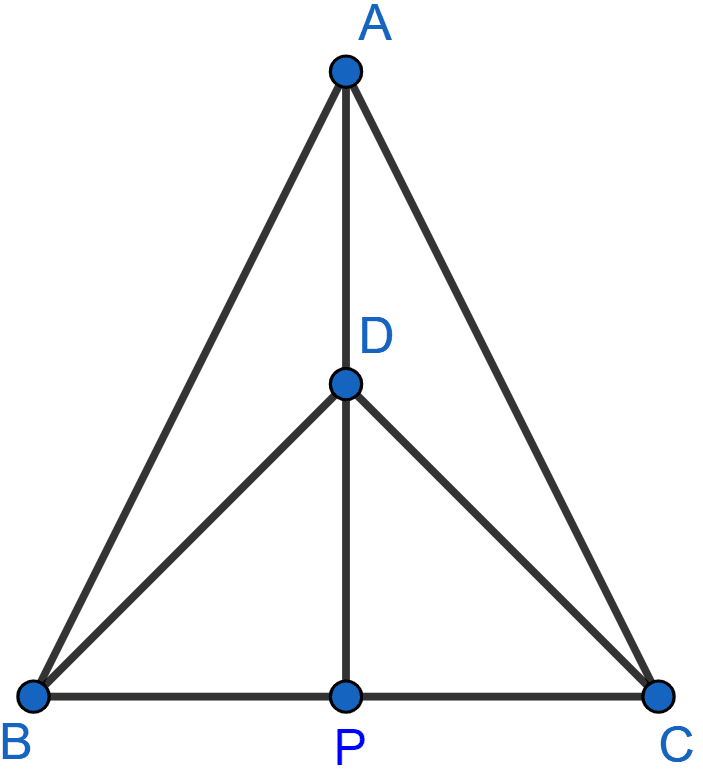
In the adjoining figure, ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that
(i) △ABD ≅ △ACD
(ii) △ABP ≅ △ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
In the adjoining figure, AP ⊥ l and PR > PQ. Show that AR > AQ.
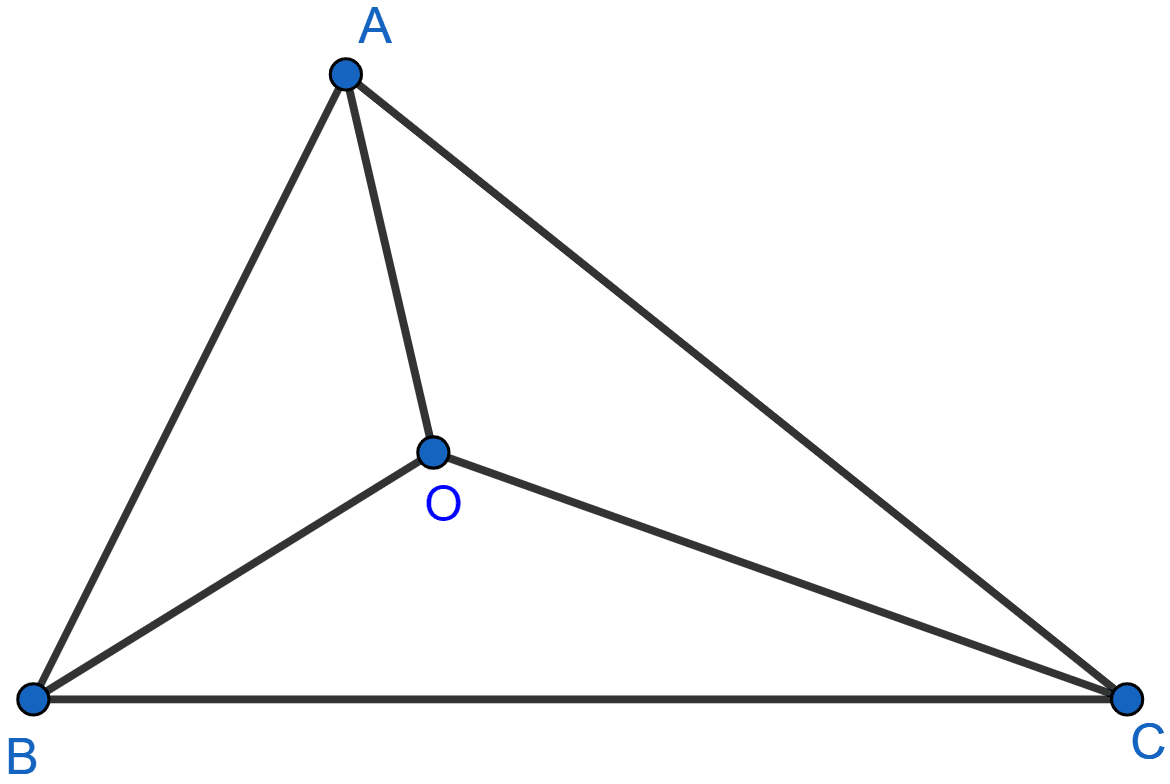
If O is any point in the interior of a triangle ABC, show that OA + OB + OC > (AB + BC + CA).