Binary search is more complicated than Linear search. But don’t worry, I will explain it to you through a real-world example then you will find it easier than Linear search.
Real World Example of Binary Search

I assume you have used a dictionary to find the meaning of any word. If I want to find the meaning of the word “Search” in the dictionary, how will I do it?
One way is that I start at the first word of the dictionary and then go through all the words in order until I get to the word “Search”. But that’s not how we search a word in the dictionary, isn’t it? Dictionaries are not meant to be searched like this as it will take a lot of time.
Instead, I will open the dictionary approximately at the middle and check to see whether the word “Search” comes before the page I have opened or after. I know this because words in the dictionary are arranged in alphabetical order.
If “Search” comes after the page I have opened, I will go to the middle of the right half of the dictionary and again check to see whether the word “Search” comes before this page or after. I will repeat this process until I have found the right page containing the word “Search”.
We searched the dictionary efficiently by using the fact that the words in the dictionary are arranged in alphabetical order. This method of searching is very similar to Binary search that we are going to learn about.
Binary Search Algorithm
The precondition to using Binary Search is that the array should be sorted.
Let’s take the same array that we used in Linear Search and arrange its elements in ascending order.

Like Linear Search, here too we want to check if 7 is present in the array or not using Binary Search.
Step 1
We will compare 7 with the middle element of the entire array. We find the index of middle element like this:
Middle Element Index = ( Start Index + End Index ) / 2 = (0 + 4) / 2 = 2
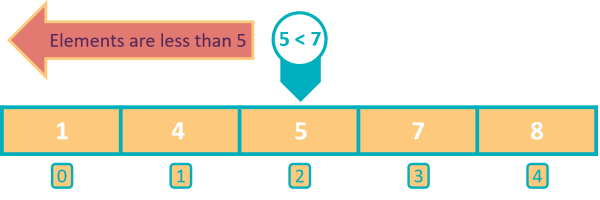
The middle element 5 is less than 7. As the array is sorted in ascending order, it is guaranteed that the elements to the left of 5 are equal to or less than 5. So, we can safely rule out the first half of the array from the beginning till index 2. 7 cannot be present in this half.
Step 2
We will focus on searching for 7 in the right part of the array. The index of middle element is:
Middle Element Index = ( Start Index + End Index ) / 2 = (3 + 4) / 2 = 3
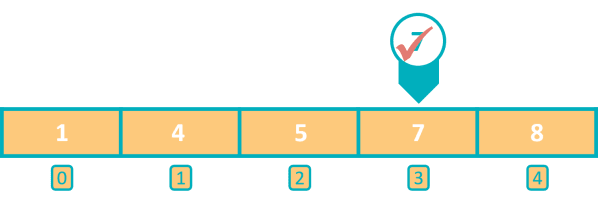
We found 7 at index 3 in the array so our search concludes successfully.
Using Binary Search, we found 7 in just 2 steps whereas with Linear Search it took us 4 steps to find 7. So Binary Search is faster than Linear Search.

But this speed comes at a cost. The array should be sorted before we can perform Binary Search on it whereas Linear Search works on sorted and unsorted arrays both.
Binary Search Java Program
Now that we have a basic understanding of Binary Search, let's look at its Java program in BlueJ and understand it’s working.
import java.util.Scanner;
public class KboatBinarySearchDemo
{
public static void main(String args[]) {
Scanner in = new Scanner(System.in);
int arr[] = {1, 4, 5, 7, 8}; //Sorted Array
System.out.print("Enter number to search: ");
int n = in.nextInt();
boolean found = false;
int l = 0, h = arr.length - 1;
int step = 1;
//Binary Search
while (l <= h) {
int m = (l + h) / 2;
/*
* These println statements are
* added for explanation only
* so that you can easily track
* the values of start index,
* end index and middle index,
* at each step of the search
*/
System.out.println("\nStep " + step++);
System.out.println("l=" + l);
System.out.println("h=" + h);
System.out.println("m=" + m);
if (arr[m] < n)
l = m + 1;
else if (arr[m] > n)
h = m - 1;
else {
System.out.println(n + " found at index "
+ m + " in the array");
found = true;
break;
}
}
if (!found)
System.out.println(n + " not found in the array");
}
}We are using the same array that we used in linear search program just that the numbers are sorted in this case as Binary Search needs a sorted array to function correctly. After that, we ask the user to enter the number he wants to search in the array. Note that, I have added a few println statements in the program so that you can easily understand how the values of start index, end index and middle index are changing at each step of the search. You can remove them in your program if you want.
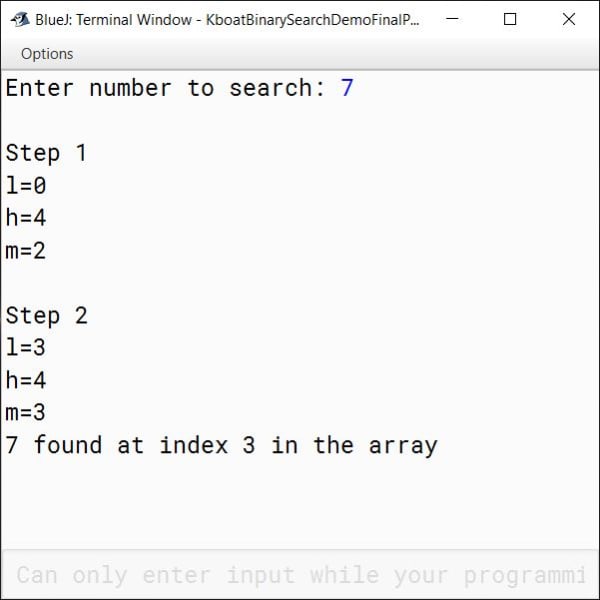
We got our output, now we will go over the program and understand it in depth.
We can visualize this array like this.

boolean found = false;
int l = 0, h = arr.length - 1;In these above lines of the Binary Search program, we first declare a boolean variable found which we will use as a flag to indicate if the search was successful or not. We initialize it to false. After that, we declare 2 int variables l and h. l holds the starting index of the part of the array in which we will do the search and h holds its ending index. In the first step, we take the middle element of the entire array so l is initialized to 0 and h to the last index of the array which is given by arr.length – 1.
//Binary Search
while (l <= h) {
int m = (l + h) / 2;
if (arr[m] < n)
l = m + 1;
else if (arr[m] > n)
h = m - 1;
else {
System.out.println(n + " found at index "
+ m + " in the array");
found = true;
break;
}
}Binary Search happens in this while loop. Note the condition of while loop, it is l less than or equal to h which means that the while loop will keep iterating as long as the start index is less than or equal to the end index. If start index becomes greater than end index, it means that we have checked all the possibilities but haven’t found the item, so the item is not present in the array.
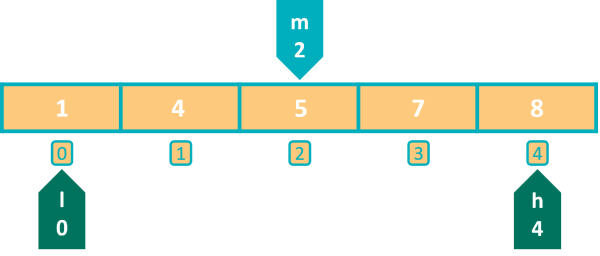
Next, we find the index of the middle element using the formula we saw earlier. m becomes 2. Then, we come to the if statement which is checking if the middle element is less than the element we are searching for. The condition is true in this case as 5 is less than 7. So, we want to search for our element only in the right part of the array. Elements to the left of index 2 are less than n.
To search in the right part of the array, I will set my start index l to one element towards the right of the middle element. We do this by setting l to m + 1. So, l becomes 3 and h is unchanged at 4. The other 2 conditions are skipped as this is an if-else-if ladder and one condition has already matched.
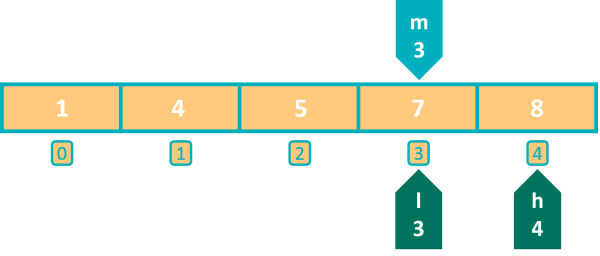
Program control goes back to the beginning of while loop. Condition is true as l is still less than h. Program control enters the while loop to start the second iteration. m becomes 3 this time. Then we check if middle element is less than n, condition tests false. We move to the else-if part and check if middle element is greater than n. Again, the condition is false, so we come to the else part. Middle element is neither less than n nor greater than n. This is possible only when it is equal to n. So, we have found our element in the array and this println statement outputs the same to the console. As we have found our element, we set the boolean variable found to true and exit the loop by executing the break statement. And with this our Binary Search program completes.
Let’s walkthrough finding another element in this array. This time I want to search for 4 in this array.
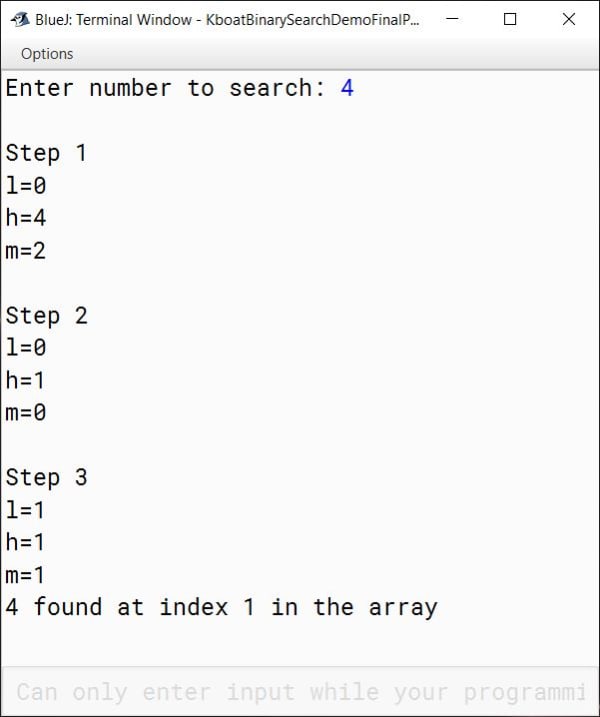
Like with searching for 7, initially l is set to 0 and h is set to 4.

Index of middle element of the array is 2. Then we check if middle element is less than n. Condition tests false this time as 5 is greater than 4. We move to the else-if condition and it tests true. This means that we should search for n only in the left part of the array as elements from index 2 and onwards are greater than n.
To search in the left part of the array, we need to set our end index at one index before the middle index. We do this by setting h to m - 1. This time the start index l is unchanged at 0.
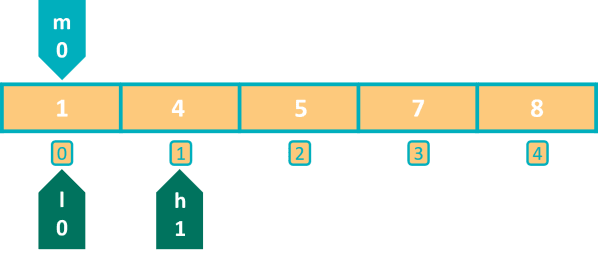
Next iteration of while loop starts, value of m is calculated as 0. Then we check if element at index 0 is less than n. Condition tests true as 1 is less than 4. We set our start index to 1.
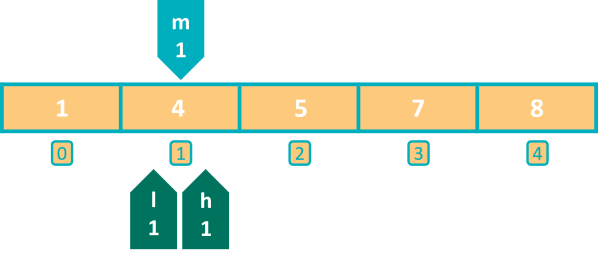
Notice that in two steps we have narrowed down our search to just a single element and in the next iteration we will find our element.
Program control goes back to the beginning of while loop. m becomes 1. Both the conditions — if (arr[m] < n) and else if (arr[m] > n) are false as element at index 1 is equal to n. Program control comes to the println statement and executes it. 4 found at index 1 in the array gets printed to the console.
So that’s how Binary Search works. It provides a lot of improvement in searching time over Linear Search but with the caveat that the array should be sorted.
Binary Search for Descending Order Array
After learning Binary Search many students get this confusion that for Binary search to work, the array needs to be sorted in ascending order only. This is not true. We can sort the array in ascending or descending order, for both cases Binary search will work. Having said that, if the array is in descending order then the Binary Search program we saw before will need some changes. It will not work as is.
Let’s change the order of the array in the Binary Search program from ascending to descending. If I execute the program now, it will give me incorrect output.
It is saying 7 not found in the array whereas 7 is present at index 1 in the array. Let’s try to understand what went wrong and what changes we should do for descending order array.
In the first iteration when the if check finds that the middle element is less than n, we search for n in the right part of the array. This was correct for ascending order but now our array is in descending order, so we need to search in the reverse direction. Instead of the right part of the array, we need to search in the left part as elements towards the right are lesser than n. So, we will change the line l = m + 1; to h = m - 1;. Similarly, when the middle element is greater than n, we need to search in the right part so we will change the line h = m - 1; to l = m + 1;. Below is the complete Binary Search program for descending order array.
//Binary Search for Descending order array
import java.util.Scanner;
public class KboatBinarySearchDemo
{
public static void main(String args[]) {
Scanner in = new Scanner(System.in);
int arr[] = {8, 7, 5, 4, 1}; //Descending Array
System.out.print("Enter number to search: ");
int n = in.nextInt();
boolean found = false;
int l = 0, h = arr.length - 1;
int step = 1;
//Binary Search
while (l <= h) {
int m = (l + h) / 2;
/*
* These println statements are
* added for explanation only
* so that you can easily track
* the values of start index,
* end index and middle index,
* at each step of the search
*/
System.out.println("\nStep " + step++);
System.out.println("l=" + l);
System.out.println("h=" + h);
System.out.println("m=" + m);
if (arr[m] < n)
h = m - 1;
else if (arr[m] > n)
l = m + 1;
else {
System.out.println(n + " found at index "
+ m + " in the array");
found = true;
break;
}
}
if (!found)
System.out.println(n + " not found in the array");
}
}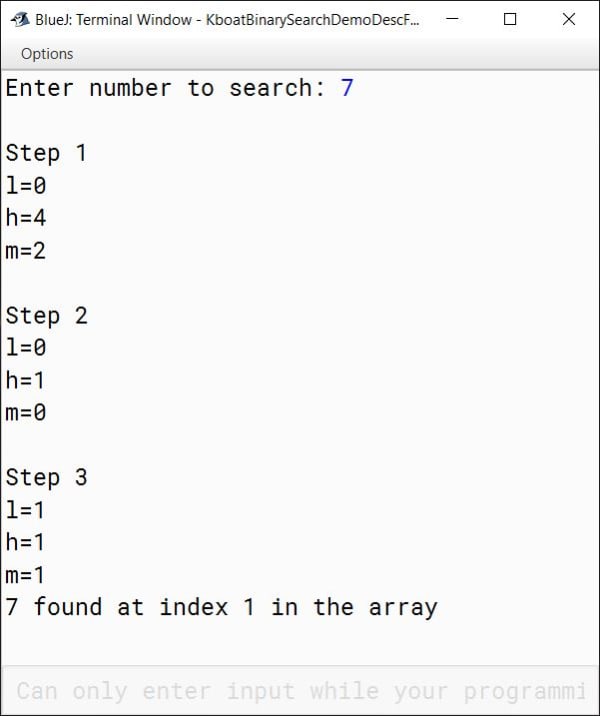
As you can see in the output above, Now it is correctly searching 7 at index 1 of the descending order array.
Differences between Binary Search and Linear Search
| Linear Search | Binary Search |
|---|---|
| Linear search works on sorted and unsorted arrays | Binary search works on only sorted arrays (ascending or descending) |
| Each element of the array is checked against the target value until the element is found or end of the array is reached | Array is successively divided into 2 halves and the target element is searched either in the first half or in the second half |
| Linear Search is slower | Binary Search is faster |