Mathematics
A mathematics teacher uses certain amount of terracotta clay to form different shaped solids. First, she turned it into a sphere of radius 7 cm and then she made a right circular cone with base radius 14 cm. Find the height of the cone so formed. If the same clay is turned to make a right circular cylinder of height cm, then find the radius of the cylinder so formed. Also, compare the total surface areas of sphere and cylinder so formed.
Mensuration
30 Likes
Answer
First, a sphere of radius (r) 7 cm is formed.
Volume of sphere =
Next, a right circular cone with radius (r1) 14 cm is formed. Let height of cone be h cm.
Since same amount of clay is used to make cone and sphere.
∴ Volume of cone = Volume of sphere
Given,
The same clay is used to make a right circular cylinder of height (h1) cm. Let its radius be r2.
Since same amount of clay is used to make cylinder and sphere.
∴ Volume of cylinder = Volume of sphere
Total surface area of sphere = 4πr2
Total surface area of cylinder = 2πr2(r2 + h1)
Hence, height of cone = 7 cm, radius of cylinder = 14 cm and Total surface area of sphere : Total surface area of cylinder = 3 : 7.
Answered By
16 Likes
Related Questions
(a) Construct the locus of a moving point which moves such that it keeps a fixed distance of 4.5 cm from a fixed-point O.
(b) Draw line segment AB of 6 cm where A and B are two points on the locus (a).
(c) Construct the locus of all points equidistant from A and B. Name the points of intersection of the loci (a) and (c) as P and Q respectively.
(d) Join PA. Find the locus of all points equidistant from AP and AB.
(e) Mark the point of intersection of the locus (a) and (d) as R. Measure and write down the length of AR.
(Use a ruler and a compass for this question.)
Construct a regular hexagon ABCDEF of side 4.3 cm and construct its circumscribed circle. Also, construct tangents to the circumscribed circle at points B and C which meets each other at point P. Measure and record ∠BPC.
(Use a ruler and a compass for this question.)
A tree (TS) of height 30 m stands in front of a tall building (AB). Two friends Rohit and Neha are standing at R and N respectively, along the same straight line joining the tree and the building (as shown in the diagram). Rohit, standing at a distance of 150 m from the foot of the building, observes the angle of elevation of the top of the building as 30°. Neha from her position observes that the top of the building and the tree has the same elevation of 60°.
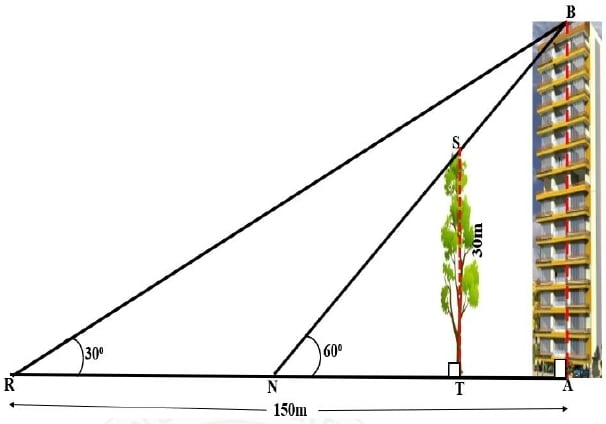
Find the:
(a) height of the building
(b) distance between
- Neha and the foot of the building
- Rohit and Neha
- Neha and the tree
- building and the tree.
A life insurance agent found the following data of age distribution of 100 policy holders, where f is an unknown frequency.
Age in years No. of policy holders 15-20 7 20-25 12 25-30 15 30-35 22 35-40 f 40-45 14 45-50 8 50-55 4 (a) If the mean age of the policy holders is 35.65 years, find the unknown frequency f.
(b) Find the median class of the distribution.