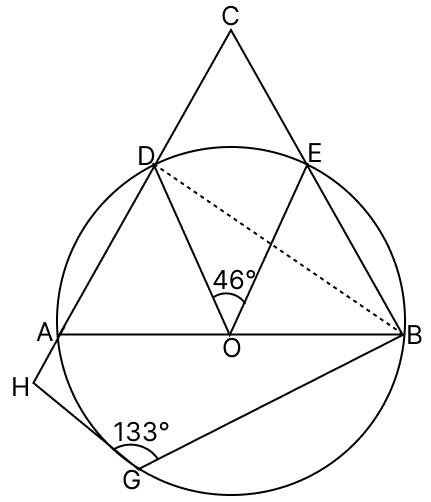
In the adjoining diagram ∠DOE = 46° and ∠BGH = 113°.

(a) Find ∠DBC and ∠DCE.

(b) Prove that CBGH is a cyclic quadrilateral.

We know that,

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

∴ ∠DBE = $\dfrac{1}{2}$ DOE

⇒ ∠DBE = $\dfrac{1}{2}$ × 46° = 23°

From figure,

⇒ ∠DBC = ∠DBE = 23°.

From figure,

⇒ ∠BDA = 90° [Angle in a semicircle]

⇒ ∠BDC = 180° - ∠BDA [Angles on a straight line]

⇒ ∠BDC = 180° - 90°

⇒ ∠BDC = 90°.

In triangle BDC,

Sum of angles in a triangle = 180°

⇒ ∠BDC + ∠DCB + ∠DBC = 180°

⇒ 90° + ∠DCB + 23° = 180°

⇒ 113° + ∠DCB = 180°

⇒ ∠DCB = 180° - 113°

⇒ ∠DCB = 67°

From figure,

∠DCE = ∠DCB = 67°.

Hence, ∠DBC = 23° and ∠DCE = 67°.

(b) From figure,

⇒ ∠BCH = ∠DCE = 67° [Common angles]

⇒ ∠BGH = 113°

⇒ ∠BGH + ∠BCH = 113° + 67° = 180°.

Since, the sum of opposite sides of quadrilateral is 180°, thus CBGH is a cyclic quadrilateral.

Hence, proved that CBGH is a cyclic quadrilateral.