Mathematics
Prove that :
Trigonometric Identities
1 Like
Answer
Solving L.H.S,
Since,
L.H.S = R.H.S
Hence, proved that
.
Answered By
1 Like
Related Questions
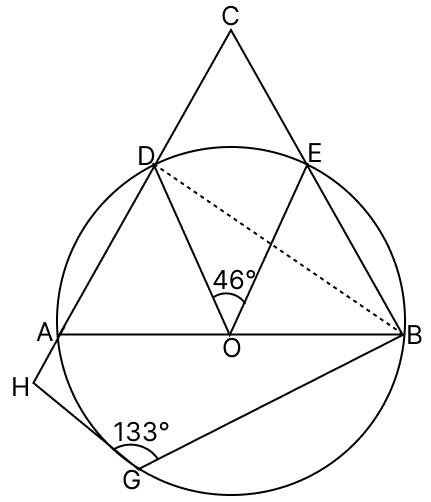
In the adjoining diagram ∠DOE = 46° and ∠BGH = 113°.
(a) Find ∠DBC and ∠DCE.
(b) Prove that CBGH is a cyclic quadrilateral.
The table given below shows a record of the weight in kilogram of 200 students of a school.
Weight(kg) Number of students 40 - 45 8 45 - 50 19 50 - 55 24 55 - 60 45 60 - 65 51 65 - 70 31 70 - 75 22 Draw a histogram and find the modal weight.
[Take 2 cm = 5 kg along one axis and 2 cm = 5 students along the other axis]
If 2x3 - 3x2 - 3x + 2 = (2x - 1)(x2 + ax + b)
(a) using Remainder and Factor theorem, find the value of ‘a’ and ‘b’.
(b) hence, factorise the polynomial 2x3 - 3x2 - 3x + 2 completely.
Using the given graph, answer the following:
(a) Write down the coordinates of the points A, B, C, and E.
(b) Name and write down the coordinates of the image of B under reflection in x-axis.
(c) Name and write the coordinates of the image of D under reflection through the origin.
(d) Which point is the image of A under reflection on the line BH? Write its coordinates.
(e) Name the closed figure ABCDEFGH.
