Mathematics
Assertion (A) : The solution set for :
x + 5 ≤ 10, if the replacement set is {x | x ≤ 5, x ∈ W} is {0, 1, 2, 3, 4, 5}.
Reason (R) : The set of elements of the replacement which satisfy the given inequation is called the solution set.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Linear Inequations
1 Like
Answer
We know that,
The set of elements of the replacement which satisfy the given inequation is called the solution set.
So, reason (R) is true.
Given,
⇒ x + 5 ≤ 10
⇒ x + 5 - 5 ≤ 10 - 5
⇒ x ≤ 5
Given,
The replacement set is {x | x ≤ 5, x ∈ W}.
∴ The solution set = {0, 1, 2, 3, 4, 5}
So, assertion (A) is true.
∴ Both A and R are correct, and R is the correct explanation for A.
Hence, option 1 is the correct option.
Answered By
1 Like
Related Questions
If x is an integer and 7 - 4x < 15, the solution set on the number line is:
1.
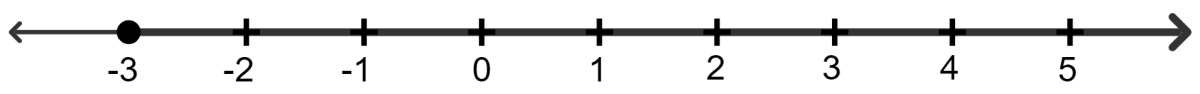
2.
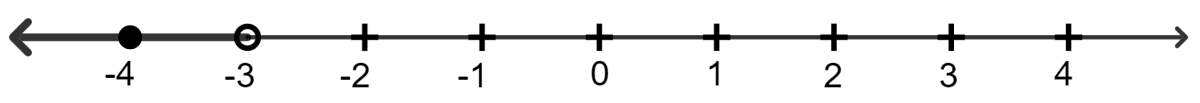
3.

4.

Statement 1: A set from which the values of the variable involved in the inequation are chosen is called the solution set.
Statement 2: A linear inequation variable (or unknown) has exactly one solution.
Which of the following options is correct?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A) : The solution set for :
x + 3 ≥ 15 is Φ, if the replacement set is {x | x < 10, x ∈ N}.
Reason (R) : If we change over the sides of an equality, we must change the sign from < to > or > to < or ≥ to ≤ or ≤ to ≥.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Assertion (A) : x < -2 and x ≥ 1.
⇒ Solution set S = {x | -2 < x ≤ 1, x ∈ R}
Reason (R) : Two inequations can be written in a combined expression.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.