Mathematics
Statement 1: A set from which the values of the variable involved in the inequation are chosen is called the solution set.
Statement 2: A linear inequation variable (or unknown) has exactly one solution.
Which of the following options is correct?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Linear Inequations
1 Like
Answer
The solution set is the set of all values that satisfy the given inequation.
The set from which the values of the variable are chosen is called the replacement set, not the solution set.
So, statement 1 is false.
A linear inequation can have multiple solutions, not just one.
For example, x > 3 has infinite solutions
So, statement 2 is false.
∴ Both the statements are false.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
If x is an integer and -4 < x ≤ 0, its solution set on the number line is:
1.

2.

3.

4.

If x is an integer and 7 - 4x < 15, the solution set on the number line is:
1.
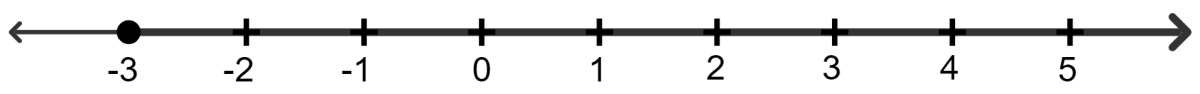
2.
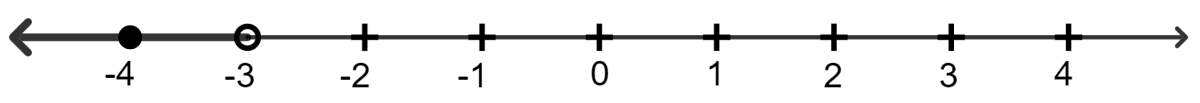
3.

4.

Assertion (A) : The solution set for :
x + 5 ≤ 10, if the replacement set is {x | x ≤ 5, x ∈ W} is {0, 1, 2, 3, 4, 5}.
Reason (R) : The set of elements of the replacement which satisfy the given inequation is called the solution set.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Assertion (A) : The solution set for :
x + 3 ≥ 15 is Φ, if the replacement set is {x | x < 10, x ∈ N}.
Reason (R) : If we change over the sides of an equality, we must change the sign from < to > or > to < or ≥ to ≤ or ≤ to ≥.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.