Physics
The circuit depicted in the figure is employed to study Ohm's Law. Rather than employing a conventional resistor, a glass tube of length ‘l’ and cross-sectional area ‘a’, which is half-filled with mercury of resistivity ‘d’, is connected to the circuit via two electrodes, E1 and E2. These electrodes are linked to a battery with an emf of ‘E’ and negligible internal resistance. Provide the answer in terms of ‘a’, ‘l’, ‘d’, and ‘E’.
(a) Resistance of mercury in the tube.
(b) The ammeter reading.
(c) Voltmeter reading.
(d) Which of the measurements are altered when the tube is entirely filled with mercury?

Current Electricity
2 Likes
Answer
Given,
Length of glass tube = l
Cross-sectional area of glass tube = a
Resistivity of mercury = d
Internal resistance of battery = 0
(a) When mercury is half filled in glass tube then cross sectional area of mercury =
Resistance of mercury in the tube:
(b) Reading of ammeter:
(c) Reading of voltmeter = E
(it does not depend on applied resistance)
(d) If mercury is entirely filled in tube then cross sectional area of mercury = a
Initially cross sectional area of mercury was
We know that:
And
By changing cross sectional area, the value of resistance and the reading of ammeter will change.
Answered By
1 Like
Related Questions
The adjacent diagram shows four solid plastic balls with wires fitted on a wooden base. A person shakes the wooden base to and fro (forward and backward) periodically. It is observed that even the balls start vibrating. It is also observed that all balls vibrate, but only one ball vibrates vigorously.
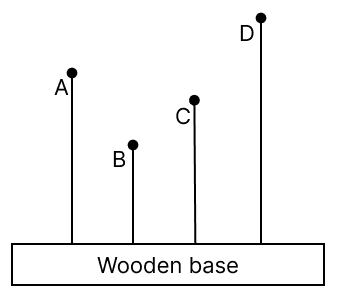
(a) Explain why only one ball vibrates vigorously.
(b) If fA, fB, fC, and fD are the natural frequencies of vibration of the wires, then arrange them in the increasing order of their frequencies and give reasons for the same.
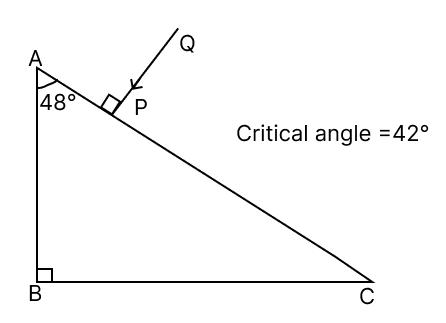
The above diagram shows a glass prism of a critical angle 42°.
(a) Redraw the diagram and complete the path of the light ray PQ till it emerges out of the prism.
(b) Also, calculate the net angle of deviation of the ray PQ when it emerges from the prism.
Two students are conducting experiments with identical 100 g mass simple pendulums, each raising the bob 5 m above the mean position. The graph depicting the relationship between distance from the mean position and velocities is presented in the diagram.

(a) Demonstrate, using mathematical calculations, that the path followed by student 1 is devoid of friction.
(b) Does the situation involving student 2 exhibit a breach of the law of conservation of energy?
Examine the graph depicting the transmitted (T) and reflected (R) waves from submarines A and B, which are equipped with a device emitting ultrasonic sounds. Study the graph and answer the following. (Speed of sound in water is 1500 m/s)
(a) Name the device used here.
(b) Why is ultrasonic sound used in this device?
(c) Which submarine is closer to the ship? Calculate the distance of the closest submarine.
