Find counter-examples to disprove the following statements:

(i) If the corresponding angles in two triangles are equal, then the triangles are congruent.

(ii) A quadrilateral with all sides equal is a square.

(iii) A quadrilateral with all angles equal is a square.

(iv) For integers a and b, $\sqrt{a^2 + b^2}$ = a + b

(v) 2n² + 11 is a prime for all whole numbers n.

(vi) n² – n + 41 is a prime for all positive integers n.

(i) Counter example :

Consider two equilateral triangle Δ ABC and Δ DEF of length 3 cm and 6 cm respectively.

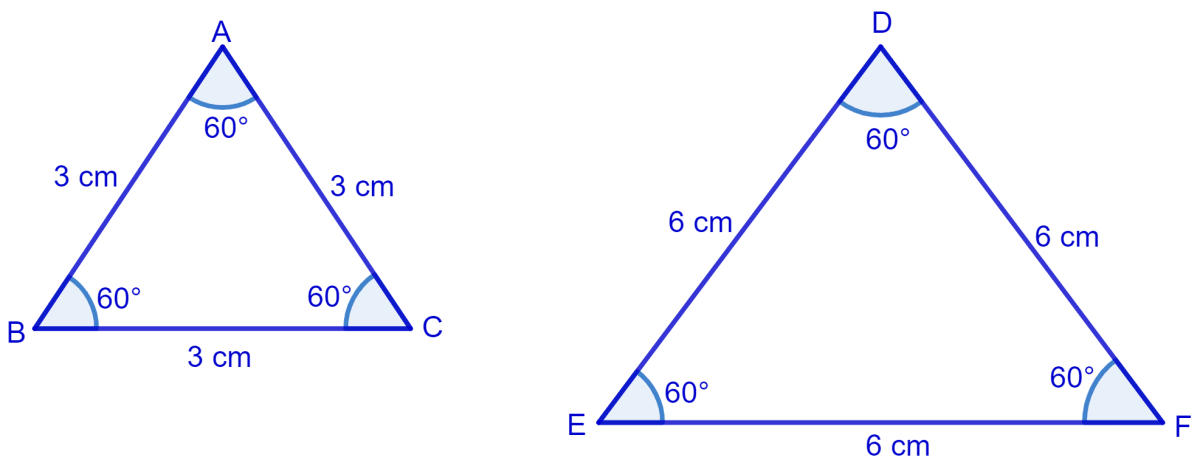
From figure,

All corresponding angles are same but sides are of different length.

∴ Δ ABC and Δ DEF are not congruent.

(ii) Counter example :

A quadrilateral with all sides equal is a rhombus which may not be a square.

(iii) Counter example :

A rectangle has all angles equal, but may not be a square.

(iv) Given,

Equation : $\sqrt{a^2 + b^2}$ = a + b

Counter example : Let a = 3 and b = 4

Substituting value of a and b in L.H.S. of the equation, we get :

$\Rightarrow \sqrt{3^2 + 4^2} \\[1em] \Rightarrow \sqrt{9 + 16} \\[1em] \Rightarrow \sqrt{25} = 5$

Substituting value of a and b in R.H.S. of the equation, we get :

⇒ 3 + 4 = 7.

Since,

L.H.S. ≠ R.H.S.

Hence, for a = 3 and b = 4, the statement $\sqrt{a^2 + b^2}$ = a + b is not true.

(v) Given,

Equation : 2n² + 11

Counter example :

Let n = 11 (by hit and trial method)

Substituting value of n in given equation.

2n² + 11 = 2(11)² + 11

= 2 x 121 + 11

= 242 + 11 = 253.

253 is divisible by 11.

Therefore, 253 is not a prime number so given statement is false for n = 11.

Hence, for n = 11, 2n² + 11 = 253, which is not a prime number.

(vi) Given,

Equation : n² - n + 41

Counter example :

Let n = 41.

Substituting value of n in given equation, we get :

n² - n + 41 = (41)² - 41 + 41

= 1681.

1681 is not prime.

Hence, for n = 41, n² – n + 41 is not prime.